题目内容
9. 一个六边形ABCDEF纸片上剪去一个角∠BGD后,得到∠1+∠2+∠3+∠4+∠5=440°则∠BGD=80°.
一个六边形ABCDEF纸片上剪去一个角∠BGD后,得到∠1+∠2+∠3+∠4+∠5=440°则∠BGD=80°.
分析 由多边形的内角和公式,即可求得六边形ABCDEF的内角和,又由∠1+∠2+∠3+∠4+∠5=440°,即可求得∠GBC+∠C+∠CDG的度数,继而求得答案.
解答 解:∵六边形ABCDEF的内角和为:180°×(6-2)=720°,且∠1+∠2+∠3+∠4+∠5=440°,
∴∠GBC+∠C+∠CDG=720°-440°=280°,
∴∠BGD=360°-(∠GBC+∠C+∠CDG)=80°.
故答案为:80°.
点评 此题考查了多边形的内角和公式.此题难度不大,注意掌握整体思想的应用,解题的关键是根据多边形的内角和的计算公式求得多边形的内角和.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
4.如果3x=m,3y=n,那么3x+y等于( )
| A. | m+n | B. | m-n | C. | mn | D. | $\frac{m}{n}$ |
14.如图图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.∠AOB是平角,从点O引射线OC,使∠AOC:∠BOC=1:5,OD是∠BOC的角平分线,则∠COD的度数是( )
| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
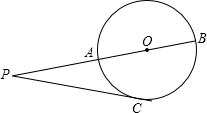 已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P、Q两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=$\frac{7}{8}$cm.
已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P、Q两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=$\frac{7}{8}$cm. 如图,将△AB C向右平移5个单位长度,再向下降2个单位长度,得到△A′B′C′,请画出平移后的图形,求△ABC的面积.
如图,将△AB C向右平移5个单位长度,再向下降2个单位长度,得到△A′B′C′,请画出平移后的图形,求△ABC的面积.