题目内容
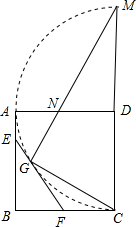
如图，圆心O在边长为
的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是
- A.
- B.
- C.
- D.
A
分析：设圆的半径为r，连接圆心与两个切点，可证明四边形OEDF是正方形，则OD=r，由BD=2，列式求出r即可．
解答：连接OE、OF，如图，
设圆的半径为r，
∴四边形OEDF是正方形，
∴OD=r，BD=2，
∵OB=r，
∴r+r=2，
解得r=2-2，
故选A．
点评：本题考查了切线的性质和勾股定理，是基础知识要熟练掌握．
分析：设圆的半径为r，连接圆心与两个切点，可证明四边形OEDF是正方形，则OD=
r，由BD=2，列式求出r即可．解答：连接OE、OF，如图，
设圆的半径为r，
∴四边形OEDF是正方形，
∴OD=
r，BD=2，∵OB=r，
∴
r+r=2，解得r=2
-2，故选A．
点评：本题考查了切线的性质和勾股定理，是基础知识要熟练掌握．
练习册系列答案
启东小题作业本系列答案
相关题目
如图所示，在边长为3的正方形ABCD中，⊙O1与⊙O2外切，且⊙O1分别于DA、DC边外切，⊙O2分别与BA、BC边外切，则圆心距，O1O2为
E作如图，圆心O在边长为
的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是（ ）
| 2 |
A、2(
| ||
B、2(
| ||
C、2
| ||
D、2
|
的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是（ ）
