题目内容
 如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=
如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=2
| ||
| 3 |
2
| ||
| 3 |
分析:作OC⊥AB于C,根据垂径定理得到AC=BC=
AB=1,再根据等腰三角形的性质易得∠A=30°,然后根据含30度的直角三角形三边的关系得到OC=
AC=
,OA=2OC=
.
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解答: 解:作OC⊥AB于C,如图,
解:作OC⊥AB于C,如图,
则AC=BC=
AB=
×2=1,
∵OA=OB,
而∠AOB=120°,
∴∠A=30°,
∴OC=
AC=
,
∴OA=2OC=
(cm).
故答案为
.
 解:作OC⊥AB于C,如图,
解:作OC⊥AB于C,如图,则AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
∵OA=OB,
而∠AOB=120°,
∴∠A=30°,
∴OC=
| ||
| 3 |
| ||
| 3 |
∴OA=2OC=
2
| ||
| 3 |
故答案为
2
| ||
| 3 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA为半径的圆交AB于D点,若AC=6,求弧AD的长.
如图,在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA为半径的圆交AB于D点,若AC=6,求弧AD的长.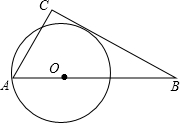 如图,在△ABC中,∠B=30°,∠C=90°,AC=6,O是AB边上的一动点,以O为圆心,OA为半径画圆.
如图,在△ABC中,∠B=30°,∠C=90°,AC=6,O是AB边上的一动点,以O为圆心,OA为半径画圆.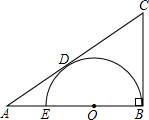 与AC切于点D.当AD2+AE2=5时,AD、AE(AD>AE)是关于x的方程x2-(m-1)x+m-2=0(m≠0)的两个根.
与AC切于点D.当AD2+AE2=5时,AD、AE(AD>AE)是关于x的方程x2-(m-1)x+m-2=0(m≠0)的两个根. 29、如图,在△ABC中,AB=AC,E是AB的中点.以点E为圆心,EB为半径画弧,交BC于点D,连接ED,井延长ED到点F,使DF=DE,连接FC.求证:∠F=∠A.
29、如图,在△ABC中,AB=AC,E是AB的中点.以点E为圆心,EB为半径画弧,交BC于点D,连接ED,井延长ED到点F,使DF=DE,连接FC.求证:∠F=∠A. 如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点,如果AB=8cm,小圆半径为3cm,那么大圆半径为
如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点,如果AB=8cm,小圆半径为3cm,那么大圆半径为