题目内容
已知:面积为16的△ABC中两中线AD⊥BE,若AD:BE=2:3,则BE=
- A.2
- B.4
- C.6
- D.8
C
分析:由于三角形的中线把三角形分成面积相等的两部分,则有△ABD和△ADC的面积相等,均为8,而AD⊥BE,有S△ABD= AD•
AD• BE=8,再把AD:BE=2:3变形后代入,即可求得BE的值.
BE=8,再把AD:BE=2:3变形后代入,即可求得BE的值.
解答: 解:如图:AD与BE交于点F.
解:如图:AD与BE交于点F.
∵AD与BE交于点F,
∴点F是三角形的重心,
∴BF= BE,
BE,
∴AD是中线,△ABC的面积为16,
∴S△ABD=S△ADC=8.
∵AD⊥BE,
∴S△ABD= AD•BF=
AD•BF= AD•
AD• BE=8①,
BE=8①,
∵AD:BE=2:3,
∴AD= BE②,
BE②,
把②代入①得:BE=6.
故选C.
点评:本题利用了中线的性质、重心的性质和三角形的面积公式求解.
分析:由于三角形的中线把三角形分成面积相等的两部分,则有△ABD和△ADC的面积相等,均为8,而AD⊥BE,有S△ABD=
 AD•
AD• BE=8,再把AD:BE=2:3变形后代入,即可求得BE的值.
BE=8,再把AD:BE=2:3变形后代入,即可求得BE的值.解答:
 解:如图:AD与BE交于点F.
解:如图:AD与BE交于点F.∵AD与BE交于点F,
∴点F是三角形的重心,
∴BF=
 BE,
BE,∴AD是中线,△ABC的面积为16,
∴S△ABD=S△ADC=8.
∵AD⊥BE,
∴S△ABD=
 AD•BF=
AD•BF= AD•
AD• BE=8①,
BE=8①,∵AD:BE=2:3,
∴AD=
 BE②,
BE②,把②代入①得:BE=6.
故选C.
点评:本题利用了中线的性质、重心的性质和三角形的面积公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知:面积为16的△ABC中两中线AD⊥BE,若AD:BE=2:3,则BE=( )
| A、2 | B、4 | C、6 | D、8 |
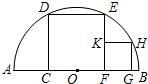 23、如图,AB是半圆O的直径,四边形CDEF是内接正方形.
23、如图,AB是半圆O的直径,四边形CDEF是内接正方形.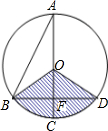 如图,已知在⊙O中,OB=4,AC是⊙O的直径,AC⊥BD 于F,图中阴影部分的面积为
如图,已知在⊙O中,OB=4,AC是⊙O的直径,AC⊥BD 于F,图中阴影部分的面积为