Question

已知等腰三角形底边上的高为4，周长为16，则这个三角形面积为

12

．

Answer 1

分析：作出图形，根据等腰三角形的三线合一的性质可得BD=

1

2

BC，设BD=x，根据三角形的周长表示出AB，然后利用勾股定理列式求出BD的长，再求出BC的长，然后利用三角形的面积公式列式进行计算即可得解．

解答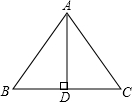：解：如图，∵AD是底边BC上的高，
∴BD=

1

2

BC，
设BD=x，
∵△ABC的周长为16，
∴AB+BD=

1

2

×16=8，
∴AB=8-x，
在Rt△ABD中，AB²=BD²+AD²，
即（8-x）²=x²+4²，
解得x=3，
∴BC=2BD=2×3=6，
∴三角形面积=

1

2

BC•AD=

1

2

×6×4=12．
故答案为：12．

点评：本题主要考查了等腰三角形三线合一的性质，勾股定理的应用，根据勾股定理列出方程是解题的关键．