Question

（2013•道里区一模）如图，在平面直角坐标系内，点O为坐标原点，直线y=-x+5交x轴于点A，交y轴于点B，直线CD交x轴负半轴于点C，交y轴正半轴于点D，直线CD交AB于点E，过点E作x轴的垂线，点F为垂足，若EF=3，tan∠ECF=

1

2

（1）求直线CD的解析式；
（2）横坐标为t的点P在CD（点P不与点C，点D重合）上，过点P作x轴的平行线交AB于点G，过点G作AB的垂线交y轴于点H，设线段OH的长为d，求d与t之间的函数关系式，并直接写出自变量t的取值范围；
（3）在（2）的条件下，当t为何值时，OH的中点在以PF为直径的圆上？

Answer 1

分析：（1）根据已知条件“过点E作x轴的垂线，点F为垂足，若EF=3”求得点E的横坐标，然后将其代入直线AB的方程即可求得点E的纵坐标，再由tan∠ECF=

1

2

求得点C的坐标；所以将点C、E的坐标分别代入直线CD的解析式为y=kx+b（k≠0），利用待定系数法求得k、b的值即可；
（2）根据题意知，-4＜t＜0．如图1，设PG交y轴于点M．根据等腰直角△BGH“三合一”的性质推知BM=MG=MH=5-（

1

2

t+2）=-

1

2

t+3，然后结合t的取值范围知点H在y轴的负半轴上，再由图形中线段间的和差关系求得以t表示的线段OH的长度d；
（3）通过相似三角形△PMN∽△NOF的对应边成比例得到

PM

NO

=

MN

OF

，因为PM=t，NO=

OH

2

=

1-t

2

，MN=

1-t

2

+

1

2

t+2=

5

2

，所以将相关线段的长度代入该比例式即可求得t的值．

解答：解：（1）∵EF=3，EF⊥x轴，
∴点E的纵坐标是3，
又∵点E在直线y=-x+5上，
∴E（2，3），则F（2，0）．
∵tan∠ECF=

1

2

，
∴

EF

FC

=

1

2

，则FC=6．
∴OC=FC-OF=6-2=4，即C（-4，0）．
设直线CD的解析式为：y=kx+b（k≠0），则

3=2k+b 0=-4k+b

，
解得

k= 1 2 b=2

．
∴直线CD的解析式为：y=

1

2

x+2；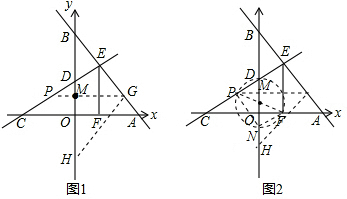

（2）根据题意知，-4＜t＜0．
如图1，设PG交y轴于点M．
∵点P在直线CD上，
∴P（t，

1

2

t+2），
∴M（0，

1

2

t+2），
由直线y=-x+5交x轴于点A，交y轴于点B，易求A（5，0），B（0，5），
∴OA=OB=5，
∴∠OBA=∠OAB=45°．
∵PG∥x轴，GH⊥AB，
∴∠MGB=∠MGH=45°，
∴BM=MG=MH=5-（

1

2

t+2）=-

1

2

t+3，
∵-4＜t＜0，
∴BM＞3，
∴BH＞6＞OB，
∴点H在y轴的负半轴上，
∴OH=MH-OM，即d=-

1

2

t+3-（

1

2

t+2）=-t+1（-4＜t＜0），
∴d与t之间的函数关系式是d=-t+1（-4＜t＜0）；

（3）如图2，设OH的中点为N．根据题意得∠PNF=90°，
∴∠PNM+∠FNO=90°．
∵∠FNO+∠OFN=90°，
∴∠PNM=∠OFN．
又∵∠PMN=∠NOF=90°，
∴△PMN∽△NOF，
∴

PM

NO

=

MN

OF

∵PM=t，NO=

OH

2

=

1-t

2

，MN=

1-t

2

+

1

2

t+2=

5

2

，
∴

-t

1-t 2

=

5 2

2

，
解得t=-

5

3

．
∴当t=-

5

3

时，OH的中点在以PF为直径的圆上．

点评：本题考查了一次函数综合题．其中涉及到的知识点有待定系数法求一次函数解析式，坐标与图形的性质，相似三角形的判定与性质以及圆周角定理等．综合性较强，难度较大．