题目内容
已知:在△AOB与△COD中,OA=OB,OC=OD,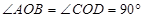 .
.
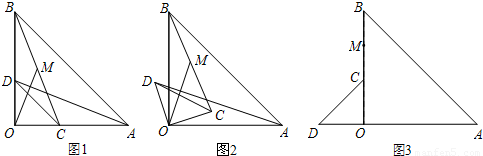
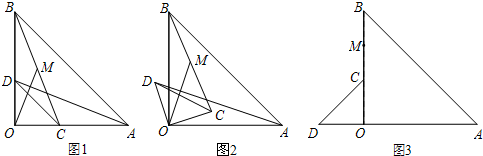
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则线段AD与OM之间的数量关系是 ,位置关系是 ;
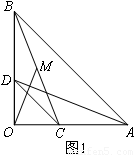
(2)如图2,将图1中的△COD绕点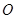 逆时针旋转,旋转角为
逆时针旋转,旋转角为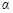 (
(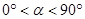 ).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
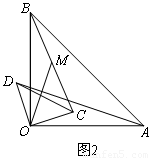
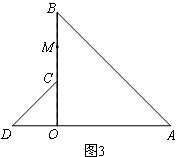
(3)如图3,将图1中的 △COD绕点 O逆时针旋转到使 △COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.
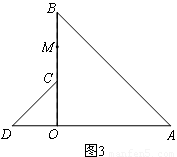
请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
(1)AD=2OM, ;(2)成立;(3)没有
;(2)成立;(3)没有
【解析】
试题分析:(1)根据直角三角形斜边的中线等于斜边的一半再结合全等三角形的性质求解即可;
(2)
延长BO到F,使FO=BO,连结CF,由题意可得MO为 的中位线,根据三角形的中位线的性质可得FC=2OM,证得△AOD≌△FOC,可得FC=AD,
的中位线,根据三角形的中位线的性质可得FC=2OM,证得△AOD≌△FOC,可得FC=AD, =
= ,再结合
,再结合 +
+ =90°,即可得到
=90°,即可得到 +
+ =90°,从而可以证得结论;
=90°,从而可以证得结论;
(3)延长DC交AB于E,连结ME,过点E作 于N,由OA=OB,OC=OD,
于N,由OA=OB,OC=OD, ,可得
,可得 ,即得AE=DE,BE=CE,∠AED=90°,则有DN=AN,即得AD=2NE,再根据M为BC的中点可得
,即得AE=DE,BE=CE,∠AED=90°,则有DN=AN,即得AD=2NE,再根据M为BC的中点可得 ,即可得到四边形ONEM是矩形,从而可以证得结论.
,即可得到四边形ONEM是矩形,从而可以证得结论.
(1)线段AD与OM之间的数量关系是AD=2OM,位置关系是 ;
;
(2)(1)的两个结论仍然成立.
如图2,延长BO到F,使FO=BO,连结CF.

∵M为BC中点,O为BF中点,
∴MO为 的中位线.
的中位线.
∴FC=2OM
∵∠AOB=∠AOF=∠COD=90°,
∴∠AOD=∠FOC .
∵AO=FO,CO=DO,
∴△AOD≌△FOC.
∴FC="AD."
∴AD=2OM
∵MO为 的中位线,
的中位线,
∴MO∥CF .
∴∠MOB=∠F.
又∵ ≌
≌ ,
,
∴ =
= .
.
∵ +
+ =90°
=90°
∴ +
+ =90°
=90°
即 ;
;
(3)(1)中线段AD与OM之间的数量关系没有发生变化.
延长DC交AB于E,连结ME,过点E作 于N.
于N.

∵OA=OB,OC=OD, ,
,
∴ .
.
∴AE=DE,BE=CE,∠AED=90°.
∴DN="AN."
∴AD=2NE.
∵M为BC的中点,
∴ .
.
∴四边形ONEM是矩形.
∴NE=OM.
∴AD=2OM.
考点:旋转问题的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

 已知:在△AOB中,AB=
已知:在△AOB中,AB= .
. 
 逆时针旋转,旋转角为
逆时针旋转,旋转角为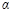 (
(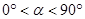 ).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;