题目内容
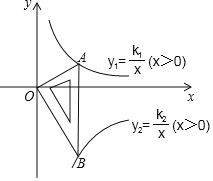
【题目】如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数y1=
（x＞0）的图象上，顶点B在函数y2=
（x＞0）的图象上，∠ABO=30°，则
= ．
【答案】
=﹣
.
【解析】
试题分析：如图，Rt△AOB中，∠B=30°，∠AOB=90°，∴∠OAC=60°，
∵AB⊥OC，∴∠ACO=90°，∴∠AOC=30°，
设AC=a，则OA=2a，OC=
a，∴A（a，a），
∵A在函数y1=
（x＞0）的图象上，∴k1=aa=a，
Rt△BOC中，OB=2OC=2a，∴BC=
=3a，∴B（a，﹣3a），
∵B在函数y2=
（x＞0）的图象上，∴k2=﹣3a·a=﹣3a，∴=﹣；
故答案为：﹣．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
