题目内容
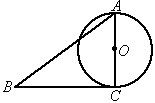
(2006辽宁沈阳课改,25)如图①,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE;②AF⊥DE.(不需要证明)

图①
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF.则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)

图②
(2)如图③,若点E、F分别在正方形ABCD的边CP的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;

图③
(3)如图④,在(2)的基础上,连接AE和EF,A若点M、N、P、Q分别为AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.

图④
答案:略
解析:
解析:
|
(1)成立 (2)成立 ∵四边形ABCD是正方形,∴∠ADF=∠DCE=90°,AD=CD. 又∵EC=DF∴ΔADF≌ΔDCE,∴∠E=∠F,AF=DE. 又∵∠E+∠CDE=90°,∴∠F+∠CDE=90°,∴∠FGD=90°,∴AF⊥DE. (3)正方形 证明:∵AM=ME,AQ=DQ ∴ MQ∥ED,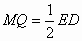 ,同理NP∥ED, ,同理NP∥ED,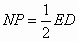 ,∴MQ ,∴MQ NP. NP.
∴四边形 MNPQ是平行四边形,又∵ME=MA,NE=NF,∴MN∥AF,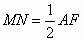 . .
又∵ AF=ED,∴MQ=MN.∴平行四边形 MNPQ是菱形.∵ AF⊥ED,MQ∥ED,∴AF⊥MQ.又∵MN∥AF,∴MN⊥MQ.∴Δ QMN=90°,∴菱形MNPQ是正方形. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ÷
÷ ,其中x=
,其中x= -4.
-4.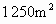 ,因为准备工作不足,第一天少拆迁了20%.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了
,因为准备工作不足,第一天少拆迁了20%.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了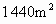 .
.
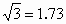 ,
, ,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.79,cos75°=0.26,tan75°=3.73.)
,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.79,cos75°=0.26,tan75°=3.73.)