��Ŀ����
��ͼ����ʾ����ֱ������ABCD�У���BAD=90�㣬E��ֱ��AB��һ�㣬��E��ֱ��l��BC����ֱ��CD�ڵ�F����ֱ��l����ƽ�ƣ���ƽ�ƾ���BEΪt��t��0����ֱ������ABCD��ֱ��lɨ���������ͼ����Ӱ���֣�ΪS��S����t�ĺ���ͼ����ͼ����ʾ��OMΪ�߶Σ�MNΪ�����ߵ�һ���֣�NQΪ���ߣ�N�������Ϊ4��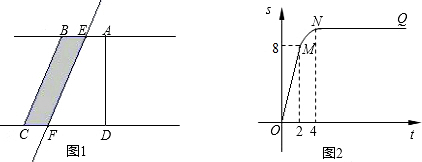
��Ϣ��ȡ
��1�������ϵij�AB=
��2��ֱ������ABCD�����=
ͼ������
��3��д��ͼ��������NQ��ʾ��ʵ�����壻
��4����2��t��4ʱ����S����t�ĺ�����ϵʽ��
������
��5����tΪ��ֵʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3��
��������1������ͼ�ڿ�֪����0��t��2ʱ��E���߶�AB���˶���������A��B�غϣ����ڴ��ڼ�E���˶���2����˿����AB�ij�Ϊ2��
��2������ͼ�ο�֪����2��t��4ʱ��E��AB���ӳ����ϣ���F��D����࣬���ڼ�E���˶���2������µ׳�Ϊ2+2=4������t=2ʱ���غϲ��ֵ����Ϊ8��������εĸ�Ϊ4��������ε����Ϊ
����2+4����4=12��
��3����t��4ʱ��ֱ��l������û�н��㣬���ɨ���������Ϊ���ε����12��
��4����2��t��4ʱ��ֱ��ɨ�����εIJ����Ǹ�����Σ������ֱ��l��AD�Ľ���Ϊ0����ô�غϲ��ֵ�����������ε������ȥ������OFD���������ã����ε�����ڣ�2�����Ѿ���ã�������OFD�У��ױ�DF=4-t����DF�ϵĸߣ�����DF�ij��͡�BCD������ֵ������ɴ˿ɵó�S��t�ĺ�����ϵʽ��
��5������Ҫ��������ۣ�
�ٵ�0��t��2ʱ���غϲ��ֵ�ƽ���ı��ε������ֱ������AEFD�����=1��3���ݴ˿����t��ֵ��
�ڵ�2��t��4ʱ���غϲ��ֵ�����ε������������OFD�����=3��1���ɴ˿����t��ֵ��
��2������ͼ�ο�֪����2��t��4ʱ��E��AB���ӳ����ϣ���F��D����࣬���ڼ�E���˶���2������µ׳�Ϊ2+2=4������t=2ʱ���غϲ��ֵ����Ϊ8��������εĸ�Ϊ4��������ε����Ϊ
| 1 |
| 2 |
��3����t��4ʱ��ֱ��l������û�н��㣬���ɨ���������Ϊ���ε����12��
��4����2��t��4ʱ��ֱ��ɨ�����εIJ����Ǹ�����Σ������ֱ��l��AD�Ľ���Ϊ0����ô�غϲ��ֵ�����������ε������ȥ������OFD���������ã����ε�����ڣ�2�����Ѿ���ã�������OFD�У��ױ�DF=4-t����DF�ϵĸߣ�����DF�ij��͡�BCD������ֵ������ɴ˿ɵó�S��t�ĺ�����ϵʽ��
��5������Ҫ��������ۣ�
�ٵ�0��t��2ʱ���غϲ��ֵ�ƽ���ı��ε������ֱ������AEFD�����=1��3���ݴ˿����t��ֵ��
�ڵ�2��t��4ʱ���غϲ��ֵ�����ε������������OFD�����=3��1���ɴ˿����t��ֵ��
����⣺������ã�
��1��AB=2��
��2��S����ABCD=12��
��3����ƽ�ƾ���BE���ڵ���4ʱ��ֱ������ABCD��ֱ��lɨ���������Ϊ12��
��4����2��t��4ʱ����ͼ��ʾ��
ֱ������ABCD��ֱ��lɨ�������S=Sֱ������ABCD-SRt��DOF
=12-
��4-t����2��4-t��=-t2+8t-4��
��5���ٵ�0��t��2ʱ����4t����12-4t��=1��3�����t=
��
�ڵ�2��t��4ʱ���У�-t2+8t-4����[12-��-t2+8t-4��]=3��1��
��t2-8t+13=0��
���t=4-
��t=4+
����ȥ����
�𣺵�t=
��t=4-
ʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3��
��1��AB=2��
��2��S����ABCD=12��
��3����ƽ�ƾ���BE���ڵ���4ʱ��ֱ������ABCD��ֱ��lɨ���������Ϊ12��

��4����2��t��4ʱ����ͼ��ʾ��
ֱ������ABCD��ֱ��lɨ�������S=Sֱ������ABCD-SRt��DOF
=12-
| 1 |
| 2 |
��5���ٵ�0��t��2ʱ����4t����12-4t��=1��3�����t=
| 3 |
| 4 |
�ڵ�2��t��4ʱ���У�-t2+8t-4����[12-��-t2+8t-4��]=3��1��
��t2-8t+13=0��
���t=4-
| 3 |
| 3 |
�𣺵�t=
| 3 |
| 4 |
| 3 |
�������������˶������⣬������ֱ�����κ�ƽ���ı��ε����ʡ�ͼ����������Լ����κ������ۺ�Ӧ�õ�֪ʶ��

��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д�
�����Ŀ
 ��ͼ��ʾ����ֱ������ABCD�У�AD��BC����B=90�㣬EF����λ�ߣ�EDƽ�֡�ADC������Ľ��ۣ���CEƽ�֡�BCD����CD=AD+BC���۵�E��CD�ľ���Ϊ
��ͼ��ʾ����ֱ������ABCD�У�AD��BC����B=90�㣬EF����λ�ߣ�EDƽ�֡�ADC������Ľ��ۣ���CEƽ�֡�BCD����CD=AD+BC���۵�E��CD�ľ���Ϊ| 1 |
| 2 |
| A��0�� | B��1�� | C��2�� | D��3�� |
 ��ͼ��ʾ����ֱ������ABCD�У���ABC=90�㣬DC��AB��BC=3��DC=4��AD=5������P�ӵ�B��������B��C��D��A�ر��˶�ʱ�����ABP��������Ϊ
��ͼ��ʾ����ֱ������ABCD�У���ABC=90�㣬DC��AB��BC=3��DC=4��AD=5������P�ӵ�B��������B��C��D��A�ر��˶�ʱ�����ABP��������Ϊ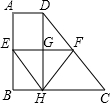 ��ͼ��ʾ����ֱ������ABCD�У�AB��BC��AD=1��BC=3��CD=4��EFΪ���ε���λ�ߣ�DHΪ���εĸ��ҽ�EF�ڵ�G�����н��ۣ���GΪEF���е㣻�ڡ�EHFΪ�ȱ������Σ����ı���EHCFΪ���Σ���S��BEH=S��CFH��������ȷ�Ľ����У�������
��ͼ��ʾ����ֱ������ABCD�У�AB��BC��AD=1��BC=3��CD=4��EFΪ���ε���λ�ߣ�DHΪ���εĸ��ҽ�EF�ڵ�G�����н��ۣ���GΪEF���е㣻�ڡ�EHFΪ�ȱ������Σ����ı���EHCFΪ���Σ���S��BEH=S��CFH��������ȷ�Ľ����У������� ��ͼ��ʾ����ֱ������ABCD�У�AD��BC����A=90�㣬AB=12��BC=21��AD=16������P�ӵ�B������������BC�ķ�����ÿ��2����λ�����ٶ��˶�������Qͬʱ�ӵ�A���������߶�AD����ÿ��1����λ�����ٶ����D�˶���������һ�����㵽��˵�ʱ��һ������Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt���룩��
��ͼ��ʾ����ֱ������ABCD�У�AD��BC����A=90�㣬AB=12��BC=21��AD=16������P�ӵ�B������������BC�ķ�����ÿ��2����λ�����ٶ��˶�������Qͬʱ�ӵ�A���������߶�AD����ÿ��1����λ�����ٶ����D�˶���������һ�����㵽��˵�ʱ��һ������Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt���룩��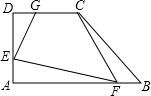 ��ͼ��ʾ����ֱ������ABCD�У���A=��D=90�㣬��ȡAE=BF=DG=x����֪AB=6��CD=3��AD=4�����ı���CGEF�����S����x�ĺ�������ʽ��x��ȡֵ��Χ��
��ͼ��ʾ����ֱ������ABCD�У���A=��D=90�㣬��ȡAE=BF=DG=x����֪AB=6��CD=3��AD=4�����ı���CGEF�����S����x�ĺ�������ʽ��x��ȡֵ��Χ��