题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 坐标为
坐标为![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 抛物线的顶点为
抛物线的顶点为![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 最小,并求出点
最小,并求出点![]() 的坐标;
的坐标;
![]() 点
点![]() 是线段
是线段![]() 上的动点,过点
上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .当
.当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 若平行于
若平行于![]() 轴的动直线
轴的动直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .问:是否存在这样的直线
.问:是否存在这样的直线![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() ;(4)的坐标为:
;(4)的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把A、C两点坐标代入抛物线解析式可求得a、c的值,可求得抛物线解析;
(2)可求得点C关于x轴的对称点C′的坐标,连接C′N交x轴于点K,再求得直线C′K的解析式,可求得K点坐标;
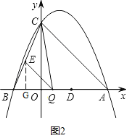
(3)过点E作EG⊥x轴于点G,设Q(m,0),可表示出AB、BQ,再证明△BQE≌△BAC,可表示出EG,可得出△CQE关于m的解析式,再根据二次函数的性质可求得Q点的坐标;
(4)分DO=DF、FO=FD和OD=OF三种情况,分别根据等腰三角形的性质求得F点的坐标,进一步求得P点坐标即可.
![]() ∵抛物线经过点
∵抛物线经过点![]() ,
,![]() ,
,
∴![]() ,解得
,解得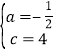 ,
,
∴抛物线解析式为![]() ;
;
![]() 由
由![]() 可求得抛物线顶点为
可求得抛物线顶点为![]() ,
,
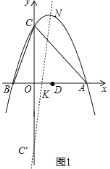
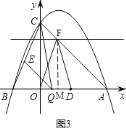
如图![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() 点即为所求,
点即为所求,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 、
、![]() 点坐标代入可得
点坐标代入可得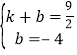 ,解得
,解得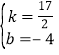 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
![]() 设点
设点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图
,如图![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
∴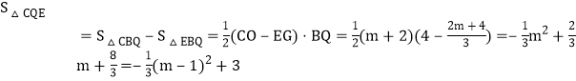 .
.
又∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,此时
,此时![]() ;
;
![]() 存在.在
存在.在![]() 中,
中,
![]() 若
若![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() .
.
又在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
此时,点![]() 的坐标为
的坐标为![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
此时,点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
![]() 若
若![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
由等腰三角形的性质得:![]() ,
,
∴![]() .
.
∴在等腰直角![]() 中,
中,![]() .
.
∴![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
此时,点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
![]() 若
若![]() ,
,
∵![]() ,且
,且![]() .
.
∴![]() .
.
∴点![]() 到
到![]() 的距离为
的距离为![]() .
.
而![]() ,与
,与![]() 矛盾.
矛盾.
∴在![]() 上不存在点使得
上不存在点使得![]() .
.
此时,不存在这样的直线![]() ,使得
,使得![]() 是等腰三角形.
是等腰三角形.
综上所述,存在这样的直线![]() ,使得
,使得![]() 是等腰三角形.所求点
是等腰三角形.所求点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案