题目内容
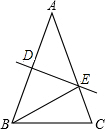 如图所示:在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E.
如图所示:在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E.(1)若∠ABE=50°,求∠EBC的度数;
(2)若△ABC的周长为41cm,边长为15cm,△BCE的周长.
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)由DE是AB的垂直平分线,根据线段垂直平分线的性质,可得AE=BE,继而求得∠A的度数,又由AB=AC,即可求得∠ABC的度数,则可求得答案;
(2)由△BCE的周长=AC+BC,然后分别从腰等于15cm与底边等于15cm去分析求解即可求得答案.
(2)由△BCE的周长=AC+BC,然后分别从腰等于15cm与底边等于15cm去分析求解即可求得答案.
解答:解:(1)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=50°,
∵AB=AC,
∴∠ABC=∠C=65°,
∴∠EBC=∠ABC-∠ABE=15°;
(2)∵AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC;
∵△ABC的周长为41cm,
∴AB+AC+BC=41cm,
若AB=AC=15cm,
则BC=11cm,
则△BCE的周长为:15+11=26cm;
若BC=15cm,则AC=AB=13cm,
∵AB>BC,
∴不符合题意,舍去.
∴△BCE的周长为26cm.
∴AE=BE,
∴∠ABE=∠A=50°,
∵AB=AC,
∴∠ABC=∠C=65°,
∴∠EBC=∠ABC-∠ABE=15°;
(2)∵AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC;
∵△ABC的周长为41cm,
∴AB+AC+BC=41cm,
若AB=AC=15cm,
则BC=11cm,
则△BCE的周长为:15+11=26cm;
若BC=15cm,则AC=AB=13cm,
∵AB>BC,
∴不符合题意,舍去.
∴△BCE的周长为26cm.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.如果设甲每小时做x个零件,那么下面所列方程中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不论a,b为任何实数,a2+b2-6a+10b+35的值总是( )
| A、非负数 | B、恒为正数 |
| C、恒为负数 | D、不等于0 |