题目内容
一辆卡车要通过跨度为8m,拱高为4m的抛物线隧道,车从隧道的正中通过,为保证安全行车,车顶到隧道顶部的距离至少要0.5米,若卡车宽1.6米,这卡车应限高多少米?
考点:二次函数的应用
专题:
分析:根据跨度求出点B的坐标,然后设抛物线顶点式形式y=ax2+4,然后把点B的坐标代入求出a的值,即可得解,再根据车的宽度为1.6,求出x=0.8时的函数值,再根据限高求出可装货物的最大高度即可.
解答: 解:∵隧道跨度为8米,隧道的顶端坐标为(O,4),
解:∵隧道跨度为8米,隧道的顶端坐标为(O,4),
∴C、D关于y轴对称,
∴OC=OD=
CD=
×8=4,
∴点D的坐标为(4,0),
设抛物线顶点式形式y=ax2+4,
把点D坐标代入得,16a+4=0,
解得a=-
,
所以,抛物线解析式为y=-
x2+4(-4≤x≤4),
当x=0.8时,y=-
×
+4=
=3.84(m),
则3.84-0.5=3.34(m).
答:这卡车应限高3.34米.
 解:∵隧道跨度为8米,隧道的顶端坐标为(O,4),
解:∵隧道跨度为8米,隧道的顶端坐标为(O,4),∴C、D关于y轴对称,
∴OC=OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴点D的坐标为(4,0),
设抛物线顶点式形式y=ax2+4,
把点D坐标代入得,16a+4=0,
解得a=-
| 1 |
| 4 |
所以,抛物线解析式为y=-
| 1 |
| 4 |
当x=0.8时,y=-
| 1 |
| 4 |
| 16 |
| 25 |
| 96 |
| 25 |
则3.84-0.5=3.34(m).
答:这卡车应限高3.34米.
点评:本题考查了二次函数的应用,主要利用了二次函数的图象的对称性,待定系数法求二次函数解析式,以及二次函数图象上点的坐标特征,比较简单.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
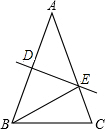 如图所示:在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E.
如图所示:在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E. 如图,∠DPC=30°,O为PC上一点,以O为圆心,2为半径作圆O,交PC于B、C两点.设PB=x,当x为何值时,圆O与PD相切?
如图,∠DPC=30°,O为PC上一点,以O为圆心,2为半径作圆O,交PC于B、C两点.设PB=x,当x为何值时,圆O与PD相切?