Question

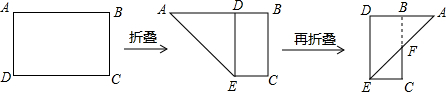
如图，有一矩形纸片ABCD，且AB：BC=3：2，先将纸片折叠，使AD落在AB边上，折痕为AE； 再将△AED以DE为折痕向右折叠，AE交BC于F．那么DB：BA等于

1. A.
   3：2
2. B.
   2：3
3. C.
   1：1
4. D.
   2：1

Answer 1

C
分析：由矩形纸片ABCD中，AB：BC=3：2，可设AB=3x，BC=2x，即可得BD=x，继而求得AB的值，则可求得答案．
解答：∵矩形纸片ABCD中，AB：BC=3：2，
∴设AB=3x，BC=2x，
则AD=BC=2x，
∴BD=AB-AD=3x-2x=x，
如图3：AB=AD-BD=2x-x=x，
∴DB：BA=x：x=1：1．
故选C．
点评：此题考查了折叠的性质以及矩形的性质．此题难度不大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．