题目内容
1.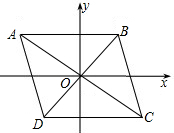 如图,?ABCD的两条对角线AC,BD相交于点O.以O为坐标原点,建立平面直角坐标系,点A的坐标为(-3,2),点B的坐标为(2,2).
如图,?ABCD的两条对角线AC,BD相交于点O.以O为坐标原点,建立平面直角坐标系,点A的坐标为(-3,2),点B的坐标为(2,2).(1)求点D,C的坐标;
(2)求S?ABCD.
分析 (1)由平行四边形的对称性得出点D与点B、点C与点A关于O对称,即可得出结果;
(2)作BE⊥CD于E,由点的坐标求出AB和BE,S?ABCD=AB•BE,即可得出结果.
解答 解:(1)∵?ABCD的两条对角线AC,BD相交于点O.O为坐标原点,
∴点D与点B、点C与点A关于原点O对称,
∵点A的坐标为(-3,2),点B的坐标为(2,2),
∴点D的坐标为(-2,-2),点C的坐标为(3,-2);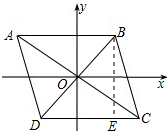 (2)作BE⊥CD于E,如图所示:
(2)作BE⊥CD于E,如图所示:
∵点A的坐标为(-3,2),点B的坐标为(2,2),
∴AB,=2+3=5,
∵点C的坐标为(3,-2),
∴BE=2+2=4,
∴S?ABCD=AB•BE=5×4=20.
点评 本题考查了平行四边形的性质、坐标与图形性质、平行四边形面积的计算方法;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
 已知:如图,点D、E分别在线段AC、AB 上,AD•AC=AE•AB,且$\frac{AD}{AE}$=$\frac{1}{2}$,S△ADB=4,试求△AEC的面积.
已知:如图,点D、E分别在线段AC、AB 上,AD•AC=AE•AB,且$\frac{AD}{AE}$=$\frac{1}{2}$,S△ADB=4,试求△AEC的面积.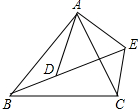 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$. 把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.
把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.