题目内容
(1)如图(1),在正方形ABCD中,对角线AC、BD相交于点O,易知AC⊥BD, =
= ;
;
(2)如图(2),若点E是正方形ABCD的边CD的中点,即 ,过D作DG⊥AE,分别交AC、BC于点F、G.求证:
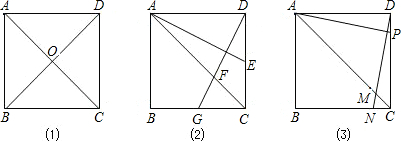
,过D作DG⊥AE,分别交AC、BC于点F、G.求证: ;
;
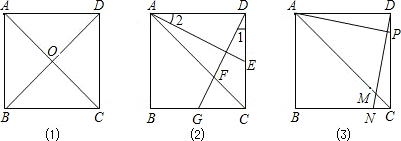
(3)如图(3),若点P是正方形ABCD的边CD上的点,且 (n为正整数),过点D作DN⊥AP,分别交AC、BC于点M、N,请你先猜想CM与AC的比值是多少,然后再证明你猜想的结论.
(n为正整数),过点D作DN⊥AP,分别交AC、BC于点M、N,请你先猜想CM与AC的比值是多少,然后再证明你猜想的结论.
 (2)证明:∵四边形ABCD为正方形,
(2)证明:∵四边形ABCD为正方形,∴AD=DC,
∴∠1+∠ADG=90°,
又∵DG⊥AE,
∴∠2+∠ADG=90°,
∴∠1=∠2,
∵AD=DC,∠1=∠2,∠ADE=∠DCG=90°,
∴△ADE≌△DCG(ASA),
∴CG=DE,
又∵E为BC中点,
∴CG=DE=
 DC,
DC,∴CG=
 AD,
AD,∵BC∥AD,
∴
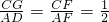 ,
,∴
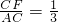 ;
;(3)猜想
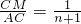 ;
;同理可证
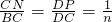 ,
,又∵BC∥AD,
∴
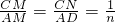 ,
,∴
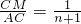 .
.分析:(2)由同角的余角知,∠1=∠2,由ASA证得△ADE≌△DCG?CG=DE,由BC∥AD?
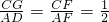 ,故有
,故有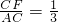 ;
;(3)同理猜想得到
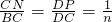 ,有
,有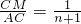 .
.点评:本题主要利用了正方形的性质,全等三角形的判定和性质和平行线的性质进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.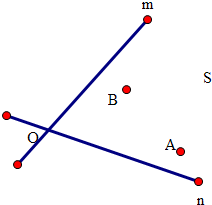 如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.(保留作图痕迹)
如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.(保留作图痕迹)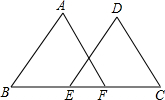 已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD
已知:如图,E、F两点在BC上,BE=CF,AB∥DE,AF∥CD 如图,已知:在△ABC中,∠A=90°,AB=AC=6,P是AB上不与A、B重合的一动点,PQ⊥BC于Q,QR⊥AC于R.
如图,已知:在△ABC中,∠A=90°,AB=AC=6,P是AB上不与A、B重合的一动点,PQ⊥BC于Q,QR⊥AC于R. 如图,一艘轮船在A处看见巡逻艇M在其北偏东64°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=
如图,一艘轮船在A处看见巡逻艇M在其北偏东64°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=