题目内容
【题目】已知抛物线经过点![]() 、
、![]() 、
、![]() .
.
(1)求抛物线的解析式;
(2)联结AC、BC、AB,求![]() 的正切值;
的正切值;
(3)点P是该抛物线上一点,且在第一象限内,过点P作![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 在点
在点![]() 的上方,且
的上方,且![]() 与
与![]() 相似时,求点P的坐标.
相似时,求点P的坐标.
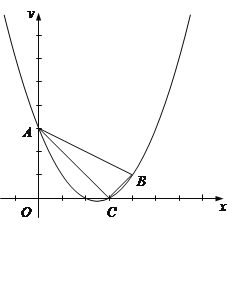
【答案】(1)![]() (2)
(2)![]() (3)点
(3)点![]() 的坐标为
的坐标为![]()
【解析】分析:(1)把A、B、C三点坐标带入抛物线解析式,利用待定系数法求解即可;
(2)由两点间的距离公式求得∴![]() 的长,由勾股定理的逆定理可判断
的长,由勾股定理的逆定理可判断![]() ,即可求得
,即可求得![]() 的值;
的值;
(3)当△APG与△ABC相似时,存在两种可能:∠PAG=∠CAB 和![]() ,分类讨论即可.
,分类讨论即可.
详解:(1)设所求二次函数的解析式为![]() ,
,
将![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )代入,得
)代入,得 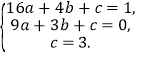
解得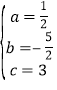 ,
,
所以,这个二次函数的解析式为![]() ;
;
(2)∵![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )
)
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ,
,
∴![]() ;
;
(3)过点P作![]() ,垂足为H,
,垂足为H,
设![]()
![]() ,则
,则![]()
![]()
∵![]() (
(![]() ,
,![]() )
)
∴![]() ,
,![]()
∵![]()
∴当△APG与△ABC相似时,存在以下两种可能:
1° ∠PAG=∠CAB 则![]()
即![]() ∴
∴![]() 解得
解得![]() ;
;
∴点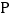 的坐标为
的坐标为![]() ;
;
2° ![]() ,则
,则![]()
即![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目