Question

学科网]

 如图，AB是⊙O的直径，点C在0O上，连接BC，AC，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．

（1)求证：DE是⊙O的切线；

(2)若，求cos∠ABC的值

Answer 1

 (1)证明：如图，连接OC．

  ∵AD是过点A的切线，AB是⊙O的直径，

  ∴AD⊥AB．

  ∴∠DAB=90⁰．

  ∵OD//BC，

  ∴∠DOC= ∠OCB. ∠AOD=∠ABC.

  ∵ OC= OB．

  ∴∠OCB=∠ABG

  ∴∠DOC=∠AOD．

   在△COD和△AOD中，

∴_△CDD≌△AOD．                

∴∠OCD=∠DAB=90⁰.

∵ OC⊥DE于点C．

∵OC是⊙O的半径，

∴DE是⊙O 的切线．              

(2)解：由 ，可设CE=2k(k>O)，则DE=3k

∴AD=DC=k[来源:Zxxk.Com]

在Rt△DAE中，AE==k   

∵OD∥BC,      

∴ BE =20B

∴0A=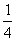AE=k     

∴ 在RRt△AOD中，OD=

∴cos∠ABC=cos∠AOD=