题目内容
14. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,BG:DG=2:3,则GH的长为$\frac{6}{5}$.
如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,BG:DG=2:3,则GH的长为$\frac{6}{5}$.
分析 根据平行线分线段成比例定理得出∴$\frac{AB}{CD}=\frac{BG}{DG}$=$\frac{2}{3}$,$\frac{GH}{CD}=\frac{BG}{BD}$=$\frac{2}{5}$,求出CD=$\frac{3}{2}$AB=3,即可求出GH的长.
解答 解:∵AB∥CH∥CD,
∴$\frac{AB}{CD}=\frac{BG}{DG}$=$\frac{2}{3}$,$\frac{GH}{CD}=\frac{BG}{BD}$=$\frac{2}{5}$,
∴CD=$\frac{3}{2}$AB=3,
∴GH=$\frac{2}{5}$CD=$\frac{6}{5}$;
故答案为:$\frac{6}{5}$.
点评 本题考查了平行线分线段成比例定理;由平行线分线段成比例定理得出比例式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
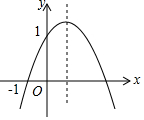 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,过点(0,1)和(-1,0),给出以下结论:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤当x>-1时,y>0;⑥8a+7b+2c-9<0其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,过点(0,1)和(-1,0),给出以下结论:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤当x>-1时,y>0;⑥8a+7b+2c-9<0其中正确结论的个数是( ) 如图,已知正方形ABCD的面积是2,则△ADE的面积是1.
如图,已知正方形ABCD的面积是2,则△ADE的面积是1. 如图,在平行四边形ABCD中,E为边CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△ABF:S△DEF=25:4.
如图,在平行四边形ABCD中,E为边CD上一点,联结AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△ABF:S△DEF=25:4.