题目内容
 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=
如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=| k | x |
分析:由A点坐标可知反比例函数解析式,再根据A、B两点坐标求直线AB的解析式,在范围内(x,y)的整数解.
解答:解:将A点坐标(1,6)代入y=
中,得k=xy=6,∴y=
,
设直线AB解析式为y=ax+b,将A(1,6),B(6,1)代入得y=-x+7,
∴当x=2时,y=
=3,y=-x+7=5,此时y=4符合条件,
当x=3时,y=
=2,y=-x+7=4,此时y=3符合条件,
当x=4时,y=
=1.5,y=-x+7=3,此时y=2符合条件,
∴符合条件的格点为(2,4),(3,3),(4,2).
故答案为:(2,4),(3,3),(4,2).
| k |
| x |
| 6 |
| x |
设直线AB解析式为y=ax+b,将A(1,6),B(6,1)代入得y=-x+7,
∴当x=2时,y=
| 6 |
| x |
当x=3时,y=
| 6 |
| x |
当x=4时,y=
| 6 |
| x |
∴符合条件的格点为(2,4),(3,3),(4,2).
故答案为:(2,4),(3,3),(4,2).
点评:本题考查了反比例函数及一次函数解析式的求法及其应用.关键是求出x=2、3、4时,两个函数对应的函数值.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
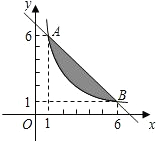 如图,A、B两点在函数y=
如图,A、B两点在函数y= 如图,A、B两点在函数
如图,A、B两点在函数
 和点C,点D是直线AC上的一个动点.
和点C,点D是直线AC上的一个动点.