题目内容
 如图,已知扇形的圆心角为120°,面积为300π.
如图,已知扇形的圆心角为120°,面积为300π.(1)求扇形的弧长;
(2)若将此扇形卷成一个圆锥,则这个圆锥的高为多少?
分析:(1)利用扇形的面积公式可得圆锥的母线长,进而利用扇形的弧长公式可得扇形的弧长;
(2)利用圆锥的侧面展开图的弧长等于圆锥的底面周长可得圆锥的底面半径,再根据勾股定理即可求出这个圆锥的高.
(2)利用圆锥的侧面展开图的弧长等于圆锥的底面周长可得圆锥的底面半径,再根据勾股定理即可求出这个圆锥的高.
解答:解:(1)设扇形的半径为R,根据题意,得 300π=
∴R2=900,
∵R>0,
∴R=30.
∴扇形的弧长=
=20π.
(2)设圆锥的底面半径为r,根据题意,得2πr=20π,
∴r=10.
h=
=20
.
答:这个圆锥的高是20
.
| 120×R2×π |
| 360 |
∴R2=900,
∵R>0,
∴R=30.
∴扇形的弧长=
| 120×30×π |
| 180 |
(2)设圆锥的底面半径为r,根据题意,得2πr=20π,
∴r=10.
h=
| 302-102 |
| 2 |
答:这个圆锥的高是20
| 2 |
点评:考查圆锥的计算;用到的知识点为:圆锥的弧长=
;圆锥的侧面展开图的弧长等于圆锥的底面周长.
| nπr |
| 180 |

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
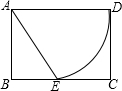 如图,已知矩形纸片ABCD,AD=2,AB=
如图,已知矩形纸片ABCD,AD=2,AB=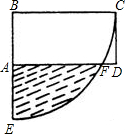 如图,已知矩形ABCD中,AB=1cm,BC=2cm,以B为圆心,BC为半径作
如图,已知矩形ABCD中,AB=1cm,BC=2cm,以B为圆心,BC为半径作

 (2012•南平模拟)如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
(2012•南平模拟)如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.