Question

如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x(m)满足关系式y=a(x-6)²+h.已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m。
（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；
（3）若球一定能越过球网，又不出边界，求h的取值范围。

Answer 1

（1）y=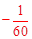 (x－6)²+2.6
（2）球能越过网；球会过界
（3）h≥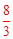

解析解：（1）把x=0，y=,及h=2.6代入到y=a(x-6)²+h，即2=a(0－6)²+2.6，∴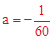 
∴当h=2.6时， y与x的关系式为y=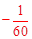 (x－6)²+2.6
（2）当h=2.6时，y=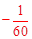 (x－6)²+2.6
∵当x=9时，y=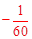 (9－6)²+2.6=2.45＞2.43，∴球能越过网。
∵当y=0时，即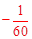 (18－x)²+2.6=0，解得x=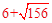＞18，∴球会过界。
（3）把x=0,y=2,代入到y=a(x-6)²+h得。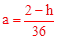
x=9时，y=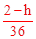 (9－6)²+h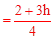＞2.43 ①
x=18时，y=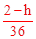 (18－6)²+h=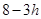≤0 ②
由①②解得h≥。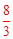
∴若球一定能越过球网，又不出边界， h的取值范围为h≥。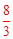
二次函数的性质和应用。
（1）利用h=2.6，将（0，2）点，代入解析式求出即可。
（2）利用h=2.6，当x=9时，y=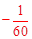 (9－6)²+2.6=2.45与球网高度比较；当y=0时，解出x值与球场的边界距离比较，即可得出结论。
（3）根据球经过点（0，2）点，得到a与h的关系式。由x=9时球一定能越过球网得到y＞2.43；由x=18时球不出边界得到y≤0。分别得出h的取值范围，即可得出答案。