Question

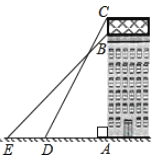
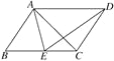
【题目】如图，点C在以AB为直径的⊙O上，BD与过点C的切线垂直于点D，BD与⊙O交于点E．

（1）求证：BC平分∠DBA；

（2）连接AE和AC，若cos∠ABD＝，OA＝m，请写出求四边形AEDC面积的思路．

Answer 1

【答案】（1）证明见解析；（2）S梯形AEDC＝m2．解题思路见解析.

【解析】

（1）如图1中，连接OC，由CD是⊙O的切线，推出OC⊥CD，由BD⊥CD，推出OC∥BD，推出∠OCB＝∠CBD，由OC＝OB，推出∠OCB＝∠OBC，即可推出∠CBO＝∠CBD；

（2）如图连接AC、AE．易知四边形AEDC是直角梯形，求出CD、AE、DE利用梯形面积公式计算即可．

（1）证明：如图1中，连接OC，

∵CD是⊙O的切线，

∴OC⊥CD，∵BD⊥CD，

∴OC∥BD，

∴∠OCB＝∠CBD，

∵OC＝OB，

∴∠OCB＝∠OBC，

∴∠CBO＝∠CBD，

∴BC平分∠DBA

（2）解：如图连接AC、AE．

∵cos∠ABD＝，

∴∠ABD＝60°，

由（1）可知，∠ABC＝∠CBD＝30°，

在Rt△ACB中，∵∠ACB＝90°，∠ABC＝30°，AB＝2m，

∴BC＝ABcos30°＝m，

在Rt△ABE中，∵∠AEB＝90°，∠BAE＝30°，AB＝2m，

∴BE＝AB＝m，AE＝m，

在Rt△CDB中，∵∠D＝90°，∠CBD＝30°，BC＝m，

∴CD＝BC＝m，BD＝m，

∴DE＝DB﹣BE＝m．

∴S梯形AEDC＝（CD+AE）DE＝m2．