题目内容
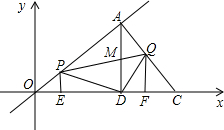
 已知:如图,在△AOB中,AB=2,C为平面内一点,且OC=3,线段OC绕点O旋转一周,连接BC,M、P分别为OA、BC的中点,则在OC旋转的过程中PM的范围为
已知:如图,在△AOB中,AB=2,C为平面内一点,且OC=3,线段OC绕点O旋转一周,连接BC,M、P分别为OA、BC的中点,则在OC旋转的过程中PM的范围为
- A.2<PM<3
- B.1<PM≤2.5
- C.0.5≤PM<3
- D.0.5≤PM≤2.5
D
分析:根据当AB∥CO时,四边形BCOA是梯形,且PM最长,以及当PM= (CO-AB)时最短即可得出答案.
(CO-AB)时最短即可得出答案.
解答: 解:当AB∥CO时,
解:当AB∥CO时,
四边形BCOA是梯形,且PM最长,
∴PM= (AB+CO)=2.5,
(AB+CO)=2.5,
如图所示,当OA′=AB=2,PM= OA,即当PM=
OA,即当PM= (CO-AB)时最短,
(CO-AB)时最短,
∴PM=0.5,
∴0.5≤PM≤2.5.
故选D.
点评:此题主要考查了旋转的性质以及三角形三边关系和梯形中位线,根据题意找出最大值与最小值是解决问题的关键.
分析:根据当AB∥CO时,四边形BCOA是梯形,且PM最长,以及当PM=
 (CO-AB)时最短即可得出答案.
(CO-AB)时最短即可得出答案.解答:
 解:当AB∥CO时,
解:当AB∥CO时,四边形BCOA是梯形,且PM最长,
∴PM=
 (AB+CO)=2.5,
(AB+CO)=2.5,如图所示,当OA′=AB=2,PM=
 OA,即当PM=
OA,即当PM= (CO-AB)时最短,
(CO-AB)时最短,∴PM=0.5,
∴0.5≤PM≤2.5.
故选D.
点评:此题主要考查了旋转的性质以及三角形三边关系和梯形中位线,根据题意找出最大值与最小值是解决问题的关键.

练习册系列答案
相关题目
 存在,请说明理由;
存在,请说明理由;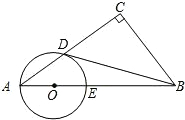 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A. 27、已知:如图,在⊙O中,OA是半径,CD是弦,OA交CD于点E.现有四个条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD.
27、已知:如图,在⊙O中,OA是半径,CD是弦,OA交CD于点E.现有四个条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD.
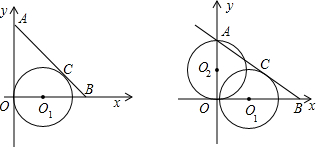 P两点,求证:O1M•O1P=2.
P两点,求证:O1M•O1P=2.