题目内容
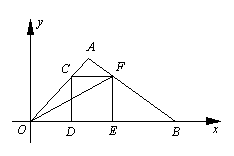
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
⑴tan∠FOB= ;
⑵ 已知二次函数图像 经过O、C、F三点,求二次函数的解析式;
经过O、C、F三点,求二次函数的解析式;
⑶ 当t为何值时以B,E,F为顶点的三角形与△OFE相似.
解:(1) 
(2) ∵图像过原点, ∴c=0
∵ 图像过c( ,
, )点
)点
∴ (0<t<2 ) ∴
(0<t<2 ) ∴  ①
①
同理图像过F(2 ,
, )点,得
)点,得  ②
②
由①②可得 =
=

∴
(3) 由△ACF~△AOB得
∴ 
要使△BEF与△OFE相似,∵∠FEO=∠FEB=90°
∴只要 或
或
即: 或
或
① 当 时,
时,  ,
,
∴ ∴
∴ (舍去)或
(舍去)或
②当 时,
时,
(ⅰ)当B在E的左侧时, ,
,
∴ ∴
∴ (舍去)或
(舍去)或
(ⅱ)当B在E的右侧时, ,
,
∴ ∴
∴ (舍去)或
(舍去)或

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

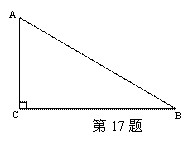
 (2)在⊿ABC中作BC的中垂线分别交AB、BC于点M、N,如果SinB=
(2)在⊿ABC中作BC的中垂线分别交AB、BC于点M、N,如果SinB= ,圆心距为
,圆心距为 ,则两圆的位置关系为( )
,则两圆的位置关系为( )