Question

【题目】如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE=AB，点P从点D出发，以每秒1个单位长度沿D→CB向终点B运动，直线EP交AD于点F，过点F作直线FG⊥DE于点G，交AB于点R.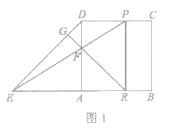

（1）求证：AF=AR;
（2）设点P运动的时间为t秒，求当选t为何值时，四边形PRBC是矩形？
（3）如图2，连接PB，请直线写出使△PRB是等腰三角形时t的值.

Answer 1

【答案】
（1）

证明：在正方形ABCD中，AD=AB=2，

∵AE=AB，

∴AD=AE，

∴∠AED=∠ADE=45°，

又∵FG⊥DE，

∴在Rt△EGR中，∠GER=∠GRE=45°，

∴在Rt△ARF中，∠FRA=∠AFR=45°，

∴AF=AR.

（2）

解：如图，当四边形PRBC是矩形时，

则有PR//BC，

∴△EAF~△ERP，

∴ ，即： 由（1）得AF=AR，

∴ ，解得：AR=-1+ 或-1- （不合题意，舍去），

∴DP=AR=-1+ ，

∵点P从点D出发，以每秒1个单位长度沿DCB向终点B运动，

∴t= -1（秒）.

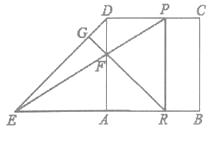
（3）

解：若PR=PB，

过点P作PK⊥AB于K，

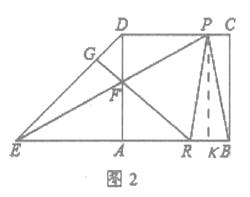
设FA=x，则RK= BR= （2-x），

∵△EFA~△EPK，

∴ ，

即： ，

解得：x=-3± （舍去负值）；

X=-3+ ，

∴t= .

若PB=RB，此时点P在BC上，

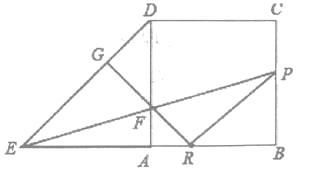
则△EFA~△EPB，

∴ ，

∴ ，

∴RB=BP= AB= ×2= ，

∴CP=BC-BP=2- = ，∴t=2+ = （秒）.

综上所述，当PR=PB时，t= ；当PB=RB时，t= 秒.

【解析】（1）在正方形ABCD中，∠FAR=90°，需要证明∠FRA=∠AFR=45°，又因为FG⊥DE，则需要证明∠AED =45°，而AE=AB=AD，则可证得；（2）当四边形PRBC是矩形时，则有PR//BC，△EAF~△ERP， ，由（1）得AF=AR，代入相关数据可解得AF，AR，又因为DP=AR所以可求得；（3）分类讨论，当点P在CD时，PB>BC=2，PR>2,RB<2,则只有PR=PB这种可能，过P作PK⊥AB于K，由（1）同理可得△EFA~△EPK，根据相似的性质解出AR边，从而解得时间t；当点P在BC时，PB<2，RB<2,则只有PB=RB这种情况，还是运用相似解出答案.
【考点精析】本题主要考查了正方形的性质的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．