��Ŀ����
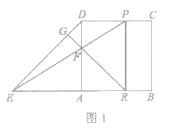
����Ŀ����ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=��1 
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������Q�ӵ�O��������ÿ��1����λ���ȵ��ٶ����߶�OM���˶���ͬʱ����M��M��O�������ÿ��3����λ���ȵ��ٶ����߶�OB���˶�������Q��x��Ĵ��߽��߶�AB�ڵ�N�����������ڵ�P�����˶���ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ���ı���OMPQΪ���Σ�
�ڡ�AON�ܷ�Ϊ���������Σ����ܣ�ֱ��д��t��ֵ�������ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������⣬�������ߵĽ���ʽΪ��y=a��x+1��2+k��
�ߵ�A��1��0����B��0��3�����������ϣ�
�� ![]() ��
��
��ã�a=��1��k=4��
�������ߵĽ���ʽΪ��y=����x+1��2+4=��x2��2x+3��
��2��
�⣺�١��ı���OMPQΪ���Σ�
��OM=PQ����3t=����t+1��2+4��
�����ã�t2+5t��3=0��
���t= ![]() ������t=
������t= ![]() ��0������ȥ��
��0������ȥ��
�൱t= ![]() ��ʱ���ı���OMPQΪ���Σ�
��ʱ���ı���OMPQΪ���Σ�
���ܣ�Rt��AOB�У�OA=1��OB=3����tanA=3��
����AON���������������������
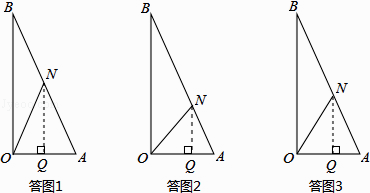
��I����ON=AN�����ͼ1��ʾ��
��QΪOA�е㣬OQ= ![]() OA=
OA= ![]() ��
��
��t= ![]() ��
��
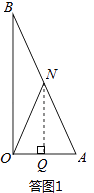
��II����ON=OA�����ͼ2��ʾ��
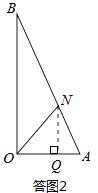
��AQ=x����NQ=AQtanA=3x��OQ=OA��AQ=1��x��
��Rt��NOQ�У��ɹ��ɶ����ã�OQ2+NQ2=ON2��
����1��x��2+��3x��2=12�����x1= ![]() ��x2=0����ȥ����
��x2=0����ȥ����
��x= ![]() ��OQ=1��x=
��OQ=1��x= ![]() ��
��
��t= ![]() ��
��
��III����OA=AN�����ͼ3��ʾ��

��AQ=x����NQ=AQtanA=3x��
��Rt��ANQ�У��ɹ��ɶ����ã�NQ2+AQ2=AN2��
����x��2+��3x��2=12�����x1= ![]() ��x2=��
��x2=�� ![]() ����ȥ����
����ȥ����
��OQ=1��x=1�� ![]() ��
��
��t=1�� ![]() ��
��
��tΪ ![]() �롢
�롢 ![]() �룬��1��
�룬��1�� ![]() ����ʱ����AONΪ���������Σ�
����ʱ����AONΪ���������Σ�
����������1�����ö���ʽ������ϵ������������ߵĽ���ʽ����2���ٵ��ı���OMPQΪ����ʱ����������OM=PQ���ݴ���һԪ���η�����⣻�ڡ�AONΪ����������ʱ�����ܴ����������Σ���Ҫ�������ۣ���һ���㣮
�����㾫�������յ��������ε������ǽ����ĸ�������Ҫ֪�����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���

 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�