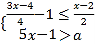题目内容
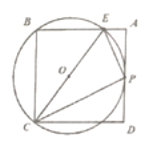
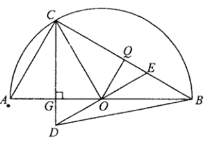
【题目】如图1,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 在半圆上,连结
在半圆上,连结![]() ,
,![]() ,且
,且![]() .连结
.连结![]() ,
,![]() 是
是![]() 边上的高,过点
边上的高,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的值.
的值.
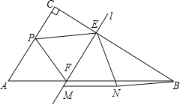
(3)如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
①若![]() ,在点
,在点![]() 运动过程中,当四边形
运动过程中,当四边形![]() 的其中一边长是
的其中一边长是![]() 的2倍时,求所有满足条件的
的2倍时,求所有满足条件的![]() 长.
长.
②连结![]() ,当
,当![]() 的面积是
的面积是![]() 的面积的3倍时,求
的面积的3倍时,求![]() 的值(请直接写出答案).
的值(请直接写出答案).
图1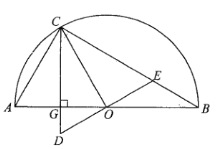 图2
图2
【答案】(1)见解析;(2)![]() ;(3)①当
;(3)①当![]() 或
或![]() 时,四边形
时,四边形![]() 其中一边长为
其中一边长为![]() 的2倍;②
的2倍;②![]()
【解析】
(1)先证明![]() 再证明
再证明![]() ,从而可得结论;
,从而可得结论;
(2)先证明![]() 是等边三角形,再证明
是等边三角形,再证明![]() ,利用锐角三角函数可得结论;(3)①分情况讨论:i当
,利用锐角三角函数可得结论;(3)①分情况讨论:i当![]() ,ii当
,ii当![]() ,iii当
,iii当![]() ,结合图形性质可得结论;②当
,结合图形性质可得结论;②当![]() 的面积是
的面积是![]() 的面积的3倍时,得到
的面积的3倍时,得到![]() 设
设![]() 则
则 ![]() 结合图形的性质用含
结合图形的性质用含![]() 的代数式表示
的代数式表示![]() 利用正切的定义可得答案.
利用正切的定义可得答案.
解:(1)∵![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,且
,且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
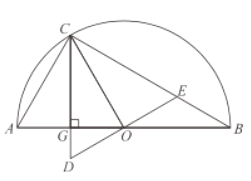
(2)∵![]() 为
为![]() 边上的高,且
边上的高,且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() 为
为![]() 中点,且
中点,且![]() ,
,
∴![]() .
.
∴![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() .
.
![]()
![]() ,
,
∴![]()
(3)①i当![]() ,由题意得:
,由题意得:
设![]() 为
为![]() ,则
,则![]()
∴![]()
由![]() ,得
,得![]()
∴![]() .
.
由![]()
得![]() .
.
∴![]()
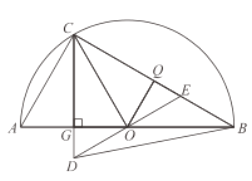
ii当![]()
设![]() 为
为![]() ,则
,则![]() .
.
由![]() 得,
得,
![]() ,化简
,化简![]() ,
,
![]() ,
,![]() (舍)
(舍)
∴![]()
iii当![]()
由于![]() ,且
,且![]()
∴不存在
综上所述,当![]() 或
或![]() 时,四边形
时,四边形![]() 其中一边长为
其中一边长为![]() 的2倍.
的2倍.
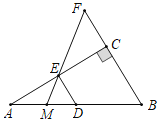
②如图,当![]() 的面积是
的面积是![]() 的面积的3倍时,
的面积的3倍时,
![]()
设![]() 则
则 ![]()
![]()
![]() 为
为![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设![]() 则
则![]()
![]()
![]()
解得:![]() 或
或![]() 舍去,
舍去,
![]()
![]()
![]()
同理可得:![]()
![]()
![]()
![]()
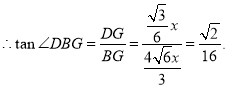

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目