Question

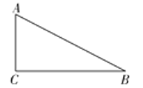
【题目】如图，在Rt△ABC中，∠ACB＝90°．

(1)请用尺规作图法，作∠ACB的平分线CD，交AB于点D；(不要求写作法，保留作图痕迹)

(2)在(1)的条件下，过点D分别作 DE⊥AC于点E，DF⊥BC于点F.求证：四边形CEDF是正方形．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）以C为圆心作圆弧，交AC，BC边于两点，在以这两点为圆心作弧相交于一点，然后连接C和这点，与AB交于点D，则AD为∠ACB的角平分线；

（2）先证四边形CEDF为矩形，再由角平分线得DE=DF，即可证明四边形CEDF为正方形.

（1）以C为圆心作圆弧，交AC，BC边于两点，在以这两点为圆心作弧相交于一点，然后连接C和这点，与AB交于点D，则AD为∠ACB的角平分线，如图所示：

（2）∵DE⊥AC，DF⊥BC，

∴∠DEC=∠DFC=90°，

∵∠ACB=90°，

∴四边形CEDF为矩形，

∵CD平分∠ACB，

∴DE=DF，

∴四边形CEDF为正方形.