题目内容
 如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=46°,则∠BDF的度数为( )
如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=46°,则∠BDF的度数为( )分析:先根据图形翻折不变性的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算即可求解.
解答:解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=46°,
∴∠BDF=180°-∠B-∠BFD=180°-46°-46°=88°.
故选A.
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=46°,
∴∠BDF=180°-∠B-∠BFD=180°-46°-46°=88°.
故选A.
点评:本题考查的是图形翻折变换的图形能够重合的性质,以及等边对等角的性质,熟知折叠的性质是解答此题的关键.

练习册系列答案
相关题目
 12、如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P,
12、如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P, 25、尺规作图(不写作法,但要保留作图痕迹)
25、尺规作图(不写作法,但要保留作图痕迹)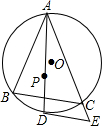 如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是
如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是 如图,点G为△ABC的重心,DE过点G,且DE∥BC,EF∥AB,那么CF:BF=
如图,点G为△ABC的重心,DE过点G,且DE∥BC,EF∥AB,那么CF:BF= 如图,点E为△ABC边AB上一点,AC=BC=BE,AE=EC,BD⊥AC于D,求∠CBD的度数.
如图,点E为△ABC边AB上一点,AC=BC=BE,AE=EC,BD⊥AC于D,求∠CBD的度数.