题目内容
已知a、b、c是△ABC的三边长,关于x的方程(b+c)x2+2ax+(c-b)=0有两个相等的实数根,且a、b是方程x2-12x+6=0的两个根,求△ABC中最长边上的高.
考点:根的判别式,根与系数的关系
专题:
分析:先根据方程有两个相等的实数根判断出△ABC是以c为斜边的直角三角形,则所求最长边上的高即为斜边上的高.再根据根与系数的关系及完全平方公式求出c的值,然后根据直角三角形的面积公式即可解答.
解答:解:∵关于x的方程(b+c)x2+2ax+(c-b)=0有两个相等的实数根,
∴△=4a2-4(b+c)(c-b)=0,即4(a2+b2-c2)=0,即a2+b2=c2,
∴此三角形是以c为斜边的直角三角形.
∵a、b是方程x2-12x+6=0的两个根,
∴a+b=12,ab=6,
∴c2=a2+b2=(a+b)2-2ab=144-12=132,
∴c=2
.
设△ABC中斜边上的高为h.
∵S△ABC=
ch=
ab,
∴h=
=
=
.
∴△=4a2-4(b+c)(c-b)=0,即4(a2+b2-c2)=0,即a2+b2=c2,
∴此三角形是以c为斜边的直角三角形.
∵a、b是方程x2-12x+6=0的两个根,
∴a+b=12,ab=6,
∴c2=a2+b2=(a+b)2-2ab=144-12=132,
∴c=2
| 33 |
设△ABC中斜边上的高为h.
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴h=
| ab |
| c |
| 6 | ||
2
|
| ||
| 11 |
点评:本题考查的是勾股定理的逆定理、根的判别式、根与系数的关系、完全平方公式及三角形的面积公式,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
方程2x+8=0的解是( )
| A、4 | B、-4 | C、3 | D、0 |
 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE的长是( )
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE的长是( )| A、2cm | B、4cm |
| C、1.2cm | D、2.4cm |
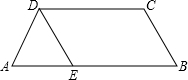 如图,已知DC∥AB,∠C=∠DEB,求证:DE∥BC.
如图,已知DC∥AB,∠C=∠DEB,求证:DE∥BC.