题目内容
 如图,机器人从A点,沿着西南方向,行了4
如图,机器人从A点,沿着西南方向,行了4| 2 |
分析:过点B作y轴的垂线,垂足为点C.
由题可知∠BAC=45°,则AC=BC=4;因为∠OBC=30°,所以OC=
,所以AO=AC+CO=4+
.
由题可知∠BAC=45°,则AC=BC=4;因为∠OBC=30°,所以OC=
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
解答: 解:过点B作y轴的垂线,垂足为点C.
解:过点B作y轴的垂线,垂足为点C.
在直角△ABC中,
∵AB=4
,∠BAC=45°,
∴AC=BC=4.
在直角△OBC中,
∠OBC=30°,∴OC=BC•tan30°=
,
∴AO=AC+CO=4+
.
∴A(0,4+
).
 解:过点B作y轴的垂线,垂足为点C.
解:过点B作y轴的垂线,垂足为点C.在直角△ABC中,
∵AB=4
| 2 |
∴AC=BC=4.
在直角△OBC中,
∠OBC=30°,∴OC=BC•tan30°=
| 4 |
| 3 |
| 3 |
∴AO=AC+CO=4+
| 4 |
| 3 |
| 3 |
∴A(0,4+
| 4 |
| 3 |
| 3 |
点评:本题考查了在平面直角坐标系中点的坐标的确定方法,注意点的坐标与对应线段的长度之间的关系.

练习册系列答案
相关题目

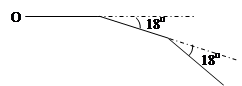

 个单位到达B点后,观察到原点O在它的南偏东60°的方向上,则原来A的坐标为 (结果保留根号).
个单位到达B点后,观察到原点O在它的南偏东60°的方向上,则原来A的坐标为 (结果保留根号).