题目内容
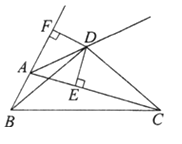
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,
交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点D在抛物线
点D在抛物线![]() 在第一象限的部分上,连接BC,DC,过点D作x轴的垂线,点E为垂足,
在第一象限的部分上,连接BC,DC,过点D作x轴的垂线,点E为垂足,![]() 的正切值等于
的正切值等于![]() 的正切值的一半,求点D的坐标;
的正切值的一半,求点D的坐标;
![]() 在
在![]() 的条件下,横坐标为t的点P在抛物线
的条件下,横坐标为t的点P在抛物线![]() 在第四象限的部分上,PB的延长线交DE于点F,连接BD,OF交于点G,连接EG,若GB平分
在第四象限的部分上,PB的延长线交DE于点F,连接BD,OF交于点G,连接EG,若GB平分![]() ,求t值.
,求t值.


【答案】(1)![]() ;(2)
;(2)![]() ;(3)t的值为2.
;(3)t的值为2.
【解析】
![]() 先确定
先确定![]() ,
,![]() ,然后利用待定系数法求抛物线解析式;
,然后利用待定系数法求抛物线解析式;
![]() 作
作![]() 于H,如图1,设
于H,如图1,设![]() ,再解方程
,再解方程![]() 得
得![]() ,利用正切的定义得到
,利用正切的定义得到![]() ,则
,则![]() ,然后解方程求出x即可得到D点坐标;
,然后解方程求出x即可得到D点坐标;
![]() 如图2,先利用待定系数法求出直线BD的解析式为
如图2,先利用待定系数法求出直线BD的解析式为![]() ,设
,设![]() ,再利用角平分线的性质定理得到GO:
,再利用角平分线的性质定理得到GO:![]() :BE,则
:BE,则![]() ,所以
,所以![]() ,解方程得到
,解方程得到![]() ,接着求出直线BD与OG的交点F的坐标为
,接着求出直线BD与OG的交点F的坐标为![]() ,然后利用待定系数法求出直线BF的解析式为
,然后利用待定系数法求出直线BF的解析式为![]() ,最后解方程组
,最后解方程组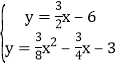 得t的值.
得t的值.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得
得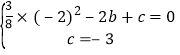 ,解得
,解得 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
![]() 作
作![]() 于H,如图1,
于H,如图1,
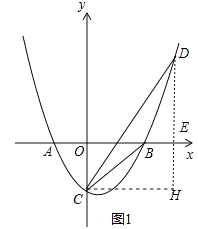
设![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() 的正切值等于
的正切值等于![]() 的正切值的一半
的正切值的一半
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,解得得
,解得得![]() ,
,![]() ,则
,则![]() ;
;
![]() 如图2,
如图2,

设直线BD的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 直线BD的解析式为
直线BD的解析式为![]() ,
,
设![]() ,
,
![]() 平分
平分![]() ,
,
![]() :
:![]() :BE,
:BE,
即GO:![]() :2,
:2,
![]() ,
,
![]() ,
,
整理得![]() ,解得
,解得![]() ,
,![]() ,
,
![]() ,
,
易得直线OF的解析式为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
设直线BF的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得
![]() 直线BF的解析式为
直线BF的解析式为![]() ,
,
解方程组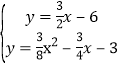 得
得![]() 或
或![]() ,
,
![]() ,
,
即t的值为2.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
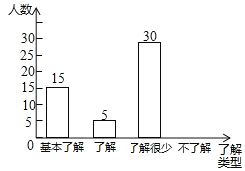
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20