题目内容
已知椭圆C的中心在原点,焦点在x轴上,且短轴的长为2,离心率等于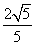 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若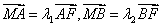 ,求证:
,求证: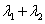 为定值。
为定值。
解:(I)设椭圆C的方程为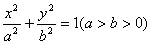 ,
,
则由题意知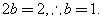 -------------------------------------------------------2分
-------------------------------------------------------2分
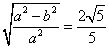
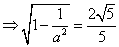
解得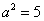 ,--------------------------------------------------------------------4分
,--------------------------------------------------------------------4分
∴椭圆C的方程为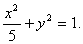 ---------------------------------------------------5分
---------------------------------------------------5分
(II)证法1:设A、B、M点的坐标分别为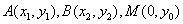 ,
,
易知F点的坐标为(2,0). ------------------------------------------------------6分
显然直线l的斜率存在,设直线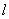 的斜率为k,则直线l的方程是
的斜率为k,则直线l的方程是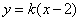 ,-----------7分
,-----------7分
将直线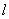 的方程代入到椭圆C的方程中,消去y并整理得
的方程代入到椭圆C的方程中,消去y并整理得
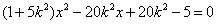 ------------------------------------------------9分
------------------------------------------------9分
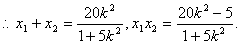 -------------------------------------------10分
-------------------------------------------10分
又
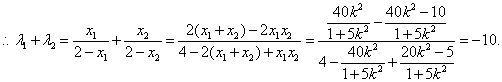 -------12分
-------12分
【证法二:设点A、B、M的坐标分别为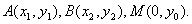
易知F点的坐标为(2,0). ------------------------------------------------------6分
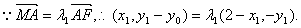 ∴
∴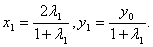 ------------7分
------------7分
将A点坐标代入到椭圆方程中,得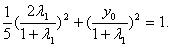 去分母整理得
去分母整理得
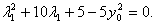 --------------------------------------------------------9分
--------------------------------------------------------9分
同理,由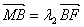 可得
可得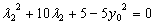 ---------------------------------10分
---------------------------------10分
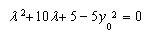
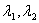 即 是方程 的两个根,
即 是方程 的两个根,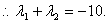 -------------------12分】
-------------------12分】

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案 ,
, ,
, 于P. 求证:
于P. 求证: .
. 
 的最大值和最小正周期分别为
的最大值和最小正周期分别为 (B)
(B) (C)
(C) (D)
(D)
 的一个面
的一个面 在半径为
在半径为 的半球底面上,A、B、C、D四个顶点都在此半球面上,则正方体
的半球底面上,A、B、C、D四个顶点都在此半球面上,则正方体 的相反数的是
的相反数的是
 ,则
,则 的值为
的值为 ,则x的取值范围是______.
,则x的取值范围是______.