题目内容
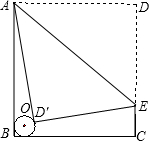 如图,一个半径为r的⊙O与矩形ABCD的两边AB、BC都相切,BC=4.若将矩形的边AD沿AE对折后和⊙O相切于点D′,折痕AE的长为5,则半径r的值为
如图,一个半径为r的⊙O与矩形ABCD的两边AB、BC都相切,BC=4.若将矩形的边AD沿AE对折后和⊙O相切于点D′,折痕AE的长为5,则半径r的值为| 4 |
| 7 |
| 4 |
| 7 |
分析:由已知及折叠定理可得AD=AD'=BC=4,根据勾股定理可得D'E=3,即得DE=3,则用r表示出OE、OG及EG,再用勾股定理得出关于r的方程,从而求出半径r的值.
解答: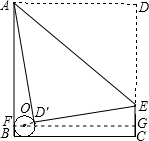 解:连接O与⊙O的切点F,并延长FO交CD与G,连接OD',
解:连接O与⊙O的切点F,并延长FO交CD与G,连接OD',
∵一个半径为r的⊙O与矩形ABCD的两边AB、BC都相切,BC=4.若将矩形的边AD沿AE对折后和⊙O相切于点D′,折痕AE的长为5,
∴AD=AD'=BC=4,
DG=AF=AD'=4,
D'E=
=
=3,
DE=D'E=3,
则OG=FG-OF=BC-OF=4-r,
OE=D'O+D'E=r+3,
EG=DG-DE=4-3=1,
在直角三角形OGE中,由勾股定理得:
OE2=EG2+OG2,
即(r+3)2=12+(4-r)2,
解得:r=
,
所以半径r的值为
.
故答案为:
.
 解:连接O与⊙O的切点F,并延长FO交CD与G,连接OD',
解:连接O与⊙O的切点F,并延长FO交CD与G,连接OD',∵一个半径为r的⊙O与矩形ABCD的两边AB、BC都相切,BC=4.若将矩形的边AD沿AE对折后和⊙O相切于点D′,折痕AE的长为5,
∴AD=AD'=BC=4,
DG=AF=AD'=4,
D'E=
| AE2-AD′2 |
| 52-42 |
DE=D'E=3,
则OG=FG-OF=BC-OF=4-r,
OE=D'O+D'E=r+3,
EG=DG-DE=4-3=1,
在直角三角形OGE中,由勾股定理得:
OE2=EG2+OG2,
即(r+3)2=12+(4-r)2,
解得:r=
| 4 |
| 7 |
所以半径r的值为
| 4 |
| 7 |
故答案为:
| 4 |
| 7 |
点评:此题考查的知识点是切线的性质、矩形的性质即折叠定理,关键是根据已知和折叠定理用r表示出OE、OG及EG,再用勾股定理求出r.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
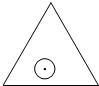 如图,一个半径为r的圆形纸片在边长为a(a≥2
如图,一个半径为r的圆形纸片在边长为a(a≥2| 3 |
A、
| ||||
B、
| ||||
C、(3
| ||||
| D、πr2 |
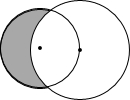
 如图,一个半径为3的圆O1的圆心经过一个半径为3
如图,一个半径为3的圆O1的圆心经过一个半径为3| 2 |
A、
| ||
| B、9 | ||
C、9π-
| ||
D、
|
 如图,一个半径为2
如图,一个半径为2