题目内容
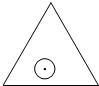 如图,一个半径为r的圆形纸片在边长为a(a≥2
如图,一个半径为r的圆形纸片在边长为a(a≥2| 3 |
A、
| ||||
B、
| ||||
C、(3
| ||||
| D、πr2 |
分析:过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,连AO1,则在Rt△ADO1中,可求得AD=
r.四边形ADO1E的面积等于三角形ADO1的面积的2倍,还可求出扇形O1DE的面积,所求面积等于四边形ADO1E的面积减去扇形O1DE的面积的三倍.
| 3 |
解答: 解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,
连AO1,则Rt△ADO1中,∠O1AD=30°,O1D=r,AD=
r.
∴S△ADO1=
O1D•AD=
r2.由S四形形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故选C.
 解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
解:如图,当圆形纸片运动到与∠A的两边相切的位置时,过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,
连AO1,则Rt△ADO1中,∠O1AD=30°,O1D=r,AD=
| 3 |
∴S△ADO1=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故选C.
点评:本题考查了面积的计算、等边三角形的性质和切线的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
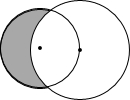
 如图,一个半径为3的圆O1的圆心经过一个半径为3
如图,一个半径为3的圆O1的圆心经过一个半径为3| 2 |
A、
| ||
| B、9 | ||
C、9π-
| ||
D、
|
 如图,一个半径为2
如图,一个半径为2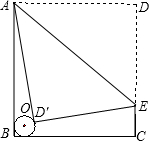 如图,一个半径为r的⊙O与矩形ABCD的两边AB、BC都相切,BC=4.若将矩形的边AD沿AE对折后和⊙O相切于点D′,折痕AE的长为5,则半径r的值为
如图,一个半径为r的⊙O与矩形ABCD的两边AB、BC都相切,BC=4.若将矩形的边AD沿AE对折后和⊙O相切于点D′,折痕AE的长为5,则半径r的值为