Question

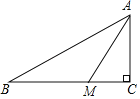
【题目】如图，Rt△ABC中，∠ACB=90°，AC=2，BC=3，点M是直线BC上一动点，且∠CAM+∠CBA=45°，则BM的长为_____．

Answer 1

【答案】或

【解析】

延长CA到E，使CE=BC=3，连接BE，作AF⊥BE，可求∠E=∠EBC=45°，根据勾股定理可求AB，AF，EF，BF的长度，可证△ABF∽△AMC，可得CM的长度，即可求BM的长度．

若点M在BC上，如图：延长CA到E，使CE＝BC＝3，连接BE，作AF⊥BE,

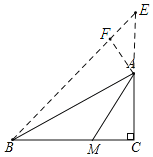
∵BC＝CE＝3，∠C＝90°，AC＝2,

∴AE＝1，∠E＝∠EBC＝45°,

∵AF⊥BE，

∴∠E＝∠EAF＝45°,

∴AF＝EF且AE＝1,

∴根据勾股定理可得EF＝AF＝,

∵BC＝3，AC＝2,

∴AB＝,

在Rt△ABF中，BF＝,

∵∠EBA+∠ABC＝45°，∠CAM+∠CBA＝45°,

∴∠MAC＝∠EBA，且∠C＝∠AFB＝90°,

∴△ABF∽△AMC,

∴,

∴CM＝,

∴BM＝BC﹣CM＝3﹣＝,

若点M在BC延长线上，可得 BM＝BC+CM＝,

故答案是：或.