题目内容
 如图,已知点G是△ABC的重心,过点G作DE∥BC,分别交边AB、AC于点D、E,那么用向量
如图,已知点G是△ABC的重心,过点G作DE∥BC,分别交边AB、AC于点D、E,那么用向量| BC |
| ED |
分析:先根据三角形重心的性质(重心到顶点的距离与重心到对边中点的距离之比为2:1),求得|
|与|
|的数量关系,然后再根据平面向量
与
的方向来确定它们之间的关系.
| BC |
| ED |
| BC |
| ED |
解答: 解:连接AG,并延长AG交BC于点F.
解:连接AG,并延长AG交BC于点F.
∵DE∥BC,
∴AG:AF=DE:BC;
又∵点G是△ABC的重心,
∴AG:AF=2:3,
∴DE:BC=2:3;即|
|:|
|=2:3;
∵向量
与向量
的方向相反,
∴
=--
;
故答案为:-
.
 解:连接AG,并延长AG交BC于点F.
解:连接AG,并延长AG交BC于点F.∵DE∥BC,
∴AG:AF=DE:BC;
又∵点G是△ABC的重心,
∴AG:AF=2:3,
∴DE:BC=2:3;即|
| ED |
| BC |
∵向量
| BC |
| ED |
∴
| ED |
| 2 |
| 3 |
| BC |
故答案为:-
| 2 |
| 3 |
| BC |
点评:本题主要考查了三角形的重心、平面向量.在解答此题时要注意两点:①三角形的重心的性质:重心到顶点的距离与重心到对边中点的距离之比为2:1,即AG:GF=2:1,而不是AG:AF=2:1;②平面向量是有方向的.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
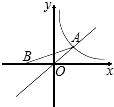 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=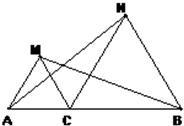 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.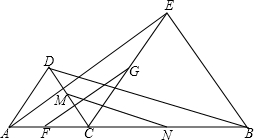 M、N分别是线段AC、CE、CD、CB的中点,
M、N分别是线段AC、CE、CD、CB的中点,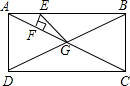 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG= 如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.
如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.