题目内容
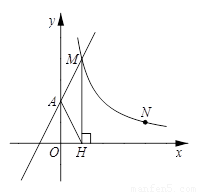
如图,直线 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO= .
. 
(1)求k的值;
(2)设点N(1,a)是反比例函数 (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(1)k="6" (2) p(0,5)
解析试题分析:
解:(1)∵直线 与y轴交于A点,∴A(0,1),OA=1
与y轴交于A点,∴A(0,1),OA=1
又∵tan∠AHO= ,∴OH=2,M横坐标为2,∴M(2,3)
,∴OH=2,M横坐标为2,∴M(2,3)
又∵点M在反比例函数图像上,∴
(2)∵点N(1,a)在反比例函数 (x>0)上,
(x>0)上,
∴点N的坐标为(1,6)
过N作N关于y轴的对称点N1,∴N1的坐标为(-1,6)
连接MN1,交x轴于P此时PM+PN最小.
设直线MN1的解析式为y=kx+b.,解得MN1的解析式为 ,
,
当x=0,得y=5,∴P点坐标为 (0,5)
考点:一次函数图像与性质,三角函数定义。对称轴的性质,
点评:熟知上述性质定义,一问较为简单,求出点M坐标代入即可,二问是最小值问题,根据对称轴的性质,两点之间线段最短,本题有一定的难度,属于中档题。

练习册系列答案
相关题目
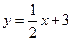 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.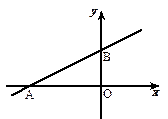
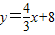 与x轴交于A点,与y轴交于B点,M是△ABO的内心,函数
与x轴交于A点,与y轴交于B点,M是△ABO的内心,函数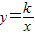 的图象经过M点,则k= .
的图象经过M点,则k= .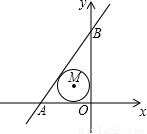
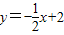 与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=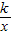 (k<0)经过点B,则k的值为( )
(k<0)经过点B,则k的值为( )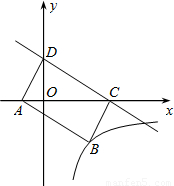
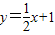 与y轴交于A点,过点A的抛物线
与y轴交于A点,过点A的抛物线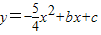 与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).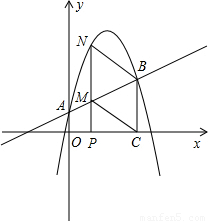
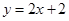 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数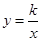 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.