题目内容
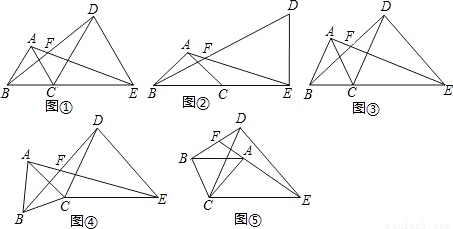
 如图,若∠C=90°,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,若∠C=90°,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC的面积为
- A.75
- B.58.5
- C.48
- D.37
B
分析:连接AE,求出AE=BE,由勾股定理求出BC=16,在Rt△ACE中,由勾股定理求出AE=BE= ,在Rt△ADE中,由勾股定理求出DE=
,在Rt△ADE中,由勾股定理求出DE= ,根据四边形ADEC的面积S=S△ACE+S△ADE代入求出即可.
,根据四边形ADEC的面积S=S△ACE+S△ADE代入求出即可.
解答: 解:连接AE.
解:连接AE.
∵AD=DB,ED⊥AB,
∴AE=BE,
在Rt△ACB中,∠C=90°,AB=20,AC=12,由勾股定理得:BC=16,
在Rt△ACE中,∠C=90°,由勾股定理得:AC2+CE2=AE2,
∴122+(16-AE)2=AE2,
解得AE=BE= ,
,
∵AD=BD= AB=10,
AB=10,
在Rt△ADE中,由勾股定理得:DE= =
= ,
,
∴四边形ADEC的面积S=S△ACE+S△ADE= ×12×(16-
×12×(16- )+
)+ ×10×
×10× =58.5.
=58.5.
故选B.
点评:本题考查了勾股定理,三角形的面积,线段垂直平分线的性质的应用,关键是求出各个线段的长.
分析:连接AE,求出AE=BE,由勾股定理求出BC=16,在Rt△ACE中,由勾股定理求出AE=BE=
 ,在Rt△ADE中,由勾股定理求出DE=
,在Rt△ADE中,由勾股定理求出DE= ,根据四边形ADEC的面积S=S△ACE+S△ADE代入求出即可.
,根据四边形ADEC的面积S=S△ACE+S△ADE代入求出即可.解答:
 解:连接AE.
解:连接AE.∵AD=DB,ED⊥AB,
∴AE=BE,
在Rt△ACB中,∠C=90°,AB=20,AC=12,由勾股定理得:BC=16,
在Rt△ACE中,∠C=90°,由勾股定理得:AC2+CE2=AE2,
∴122+(16-AE)2=AE2,
解得AE=BE=
 ,
,∵AD=BD=
 AB=10,
AB=10,在Rt△ADE中,由勾股定理得:DE=
 =
= ,
,∴四边形ADEC的面积S=S△ACE+S△ADE=
 ×12×(16-
×12×(16- )+
)+ ×10×
×10× =58.5.
=58.5.故选B.
点评:本题考查了勾股定理,三角形的面积,线段垂直平分线的性质的应用,关键是求出各个线段的长.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
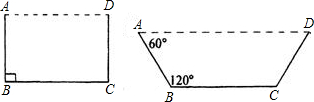 面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).
面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).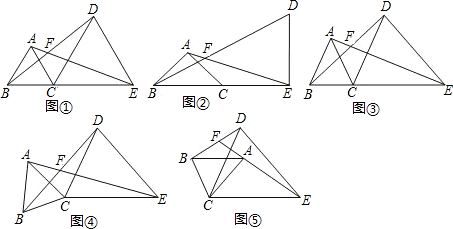
 如图,若∠C=90°,∠A=60°,AC=2m,则AB的长是( )
如图,若∠C=90°,∠A=60°,AC=2m,则AB的长是( ) 如图,若∠C=90°,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC的面积为( )
如图,若∠C=90°,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC的面积为( ) ;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.
;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.