Question

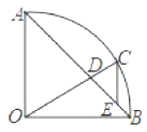
【题目】如图，O为矩形ABCD的对角线BD的中点，点E在AD上，连接EB、EO，BD平分∠EBC，点F在BE上，tan∠OFE＝tan∠ABD，若AE=3EF，CD=3，则OD的长为______．

Answer 1

【答案】

【解析】

分别过点O作OG⊥EF于点G，OM⊥BC于点M，延长MO交AD于点N，则MN⊥AD，先由等角对对边证明BE=ED．然后根据角度的相互转化得出∠BEO=∠OFE，从而有EO=FO，再根据等腰三角形三线合一的性质得出EG=FG，设EG=FG=a，用含a的式子表示出AE，BE的长，在Rt△ABE中，利用勾股定理可得出关于a的方程，从而可得出a的值，进行可得出AD的长，最后在Rt△ABD中，可求出BD的长，利用OD=BD即可得出结果．

解：分别过点O作OG⊥EF于点G，OM⊥BC于点M，延长MO交AD于点N，

∵四边形ABCD为矩形，∴∠ABC=∠C=∠A=90°，AB=CD=3，AD∥BC，

∴∠DBC=∠EDB，MN⊥AD，

∵BD平分∠EBC，∴∠EBD=∠DBC，

∴∠EBD=∠EDB，∴BE=ED，

又O为BD的中点，∴EO⊥BD，∠BEO=∠DEO．

设∠EBO=∠OBM=x，则∠ABD=90°-x，

又tan∠OFE＝tan∠ABD，

∴∠OFE=∠ABD=90°-x．

又EO⊥BD，∴∠BEO=90°-∠EBO=90°-x，

∴∠BEO=∠OFE，∴OF=OE，又OG⊥EF，∴EG=FG．

设EG=FG=a，则EF=2a，∴AE=3EF=6a，

又EO平分∠BED，OG⊥BE，ON⊥ED，∴OG=ON，又OE=OE，

∴Rt△EGO≌Rt△ENO，∴EN=EG=a，

∴AN=AE+EN=7a，

∵O为BD中点，NO∥AB，∴N为AD的中点，∴ND=AN=7a，

∴ED=EN+DN=8a=BE，

在Rt△ABE中，由勾股定理得，AE2+AB2=BE2，

（6a）2+32=（8a）2，解得a2=．

∴AD2=4AN2=4×49a2=63，

在Rt△ABD中，由勾股定理得，BD==，

∴OD=BD=．

故答案为：．