题目内容
直线y=x+6与x轴、y轴围成的三角形面积为________（平方单位）．
18
分析：分别求出直线与x轴、y轴的交点坐标，再根据直角三角形的面积公式求解即可．注意线段的长度是正数．
解答：因为直线y=x+6中，
-
=-
=-6，
∴b=6，
设直线与x轴、y轴的交点坐标分别为A（-6，0），B（0，6），
∴S△AOB=
×|-6|×6=×6×6=18，
故直线y=x+6与x轴、y轴围成的三角形面积为18．
点评：求出直线与坐标轴的交点，把求线段的长的问题转化为求函数的交点的问题．
分析：分别求出直线与x轴、y轴的交点坐标，再根据直角三角形的面积公式求解即可．注意线段的长度是正数．
解答：因为直线y=x+6中，
-
=-=-6，∴b=6，
设直线与x轴、y轴的交点坐标分别为A（-6，0），B（0，6），
∴S△AOB=
×|-6|×6=×6×6=18，故直线y=x+6与x轴、y轴围成的三角形面积为18．
点评：求出直线与坐标轴的交点，把求线段的长的问题转化为求函数的交点的问题．
练习册系列答案
相关题目
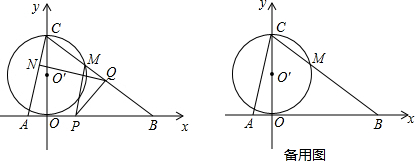
（2012•兰州）如图，M为双曲线y=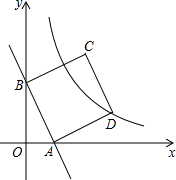
（2013•宛城区一模）如图，直线y=-2x+2与x轴y轴分别相交于点A、B，四边形ABCD是正方形，曲线y=