题目内容
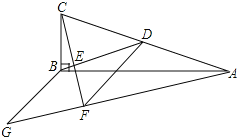
【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG为菱形;
(2)若AG=13,CF=6,求四边形BDFG的周长.
【答案】(1)证明见解析;(2)20.
【解析】
(1)由BD=FG,BD//FG可得四边形BDFG是平行四边形,根据CE⊥BD可得∠CFA=∠CED=90°,根据直角三角形斜边中线的性质可得BD=DF=![]() AC,即可证得结论;
AC,即可证得结论;
(2)设GF=x,则AF=13﹣x,AC=2x,利用勾股定理列方程可求出x的值,进而可得答案.
(1)∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,BD//AG,
∴∠CFA=∠CED=90°,
∵点D是AC中点,
∴DF=![]() AC,
AC,
∵∠ABC=90°,BD为AC的中线,
∴BD=![]() AC,
AC,
∴BD=DF,
∴平行四边形BGFD是菱形.
(2)设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,
解得:x=5,x=﹣![]() (舍去),
(舍去),
∵四边形BDFG是菱形,
∴四边形BDFG的周长=4GF=20.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
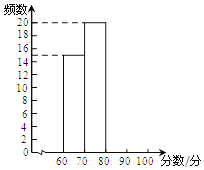
【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.