Question

【题目】在平面直角坐标系中，点C沿着某条路径运动，以点C为旋转中心，将点A（0，4）逆时针旋转90°到点B（m，1），若﹣5≤m≤5，则点C运动的路径长为__．

Answer 1

【答案】

【解析】

试题解析：如图1所示，在y轴上取点P（0，1），过P作直线l∥x轴，

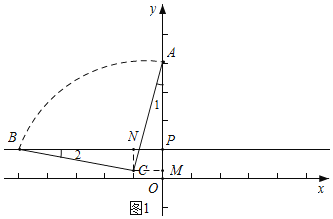
∵B（m，1），

∴B在直线l上，

∵C为旋转中心，旋转角为90°，

∴BC=AC，∠ACB=90°，

∵∠APB=90°，

∴∠1=∠2，

作CM⊥OA于M，作CN⊥l于N，则Rt△BCN≌Rt△ACM，

∴CN=CM，

若连接CP，则点C在∠BPO的平分线上，

∴动点C在直线CP上运动；

如图2所示，∵B（m，1）且-5≤m≤5，

∴分两种情况讨论C的路径端点坐标，

①当m=-5时，B（-5，1），PB=5，

作CM⊥y轴于M，作CN⊥l于N，

同理可得△BCN≌△ACM，

∴CM=CN，BN=AM，

可设PN=PM=CN=CM=a，

∵P（0，1），A（0，4），

∴AP=3，AM=BN=3+a，

∴PB=a+3+a=5，

∴a=1，

∴C（-1，0）；

②当m=5时，B（5，1），如图2中的B1，此时的动点C是图2中的C1，

同理可得C1（4，5），

∴C的运动路径长就是CC1的长，

由勾股定理可得，CC1=．