题目内容
 如图,是一条高速公路隧道的横截面,若它的形状是以O为圆心的圆的一部分,圆的半径OA=5米,高CD=8米,则路面宽AB=
如图,是一条高速公路隧道的横截面,若它的形状是以O为圆心的圆的一部分,圆的半径OA=5米,高CD=8米,则路面宽AB=
- A.5米
- B.6米
- C.7米
- D.8米
D
分析:圆中的半径相等,所以OA=OC,又CD=8,所以OD=3,所以在Rt△AOD中,根据勾股定理,可以求出AD,进而可以求出AB.
解答:∵OA=OC=5,CD=8,
∴OD=3,
∵CD⊥AB,
∴AD=BD,
在Rt△AOD中,AD=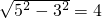 ,
,
所以AB=2AD=2×4=8米.
故选D.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+( )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
分析:圆中的半径相等,所以OA=OC,又CD=8,所以OD=3,所以在Rt△AOD中,根据勾股定理,可以求出AD,进而可以求出AB.
解答:∵OA=OC=5,CD=8,
∴OD=3,
∵CD⊥AB,
∴AD=BD,
在Rt△AOD中,AD=
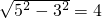 ,
,所以AB=2AD=2×4=8米.
故选D.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
 )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个. 
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,是一条高速公路隧道的横截面,若它的形状是以O为圆心的圆的一部分,圆的半径OA=5米,高CD=8米,则路面宽AB=( )
如图,是一条高速公路隧道的横截面,若它的形状是以O为圆心的圆的一部分,圆的半径OA=5米,高CD=8米,则路面宽AB=( )| A、5米 | B、6米 | C、7米 | D、8米 |


