题目内容
 如图,扇形OAB的圆心角为120°,半径为6cm.
如图,扇形OAB的圆心角为120°,半径为6cm.(1)请用尺规作出扇形的对称轴(不写作法,但应保留作图痕迹);
(2)若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的高.
分析:(1)画出圆心角的平分线;
(2)根据弧长公式计算.
(2)根据弧长公式计算.
解答:解:(1)如图
(3分)

(2)设圆锥的底面半径为r,母线为l,高为h,
则I=AO=OD=6,底面圆周长为2πr,
的长为
,
则2πr=
=4π,∴r=2(5分)
根据勾股定可得圆锥的高为h=
=4
cm(7分).
(3分)


(2)设圆锥的底面半径为r,母线为l,高为h,
则I=AO=OD=6,底面圆周长为2πr,
 |
| AB |
| 120×6π |
| 180 |
则2πr=
| 120×6π |
| 180 |
根据勾股定可得圆锥的高为h=
| l2-r2 |
| 2 |
点评:此题考查了基本作图和圆锥的相关计算,需要同学们有一定的空间想象能力.将圆锥展开即为扇形,底面圆周长即为扇形弧长,圆锥母线即为扇形半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
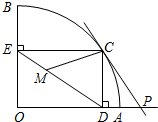 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是 (2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,

