题目内容
在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为 ;
(2)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.
(3)连接AD,当OC∥AD时,
①求出点C的坐标;②直线BC是否为⊙O的切线?请作出判断,并说明理由.

解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°;当C点在y轴右侧时,∠BOC=180°﹣∠OBA=135°;
(2)∵△OAB为等腰直角三角形,
∴AB= OA=6
OA=6 ,
,
∴当点C到AB的距离最大时,△ABC的面积最大,
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,如图,此时C点到AB的距离的最大值为CE的长,
∵△OAB为等腰直角三角形,
∴AB= OA=6
OA=6 ,
,
∴OE= AB=3
AB=3 ,
,
∴CE=OC+CE=3+3 ,△ABC的面积=
,△ABC的面积= CE•AB=
CE•AB= ×(3+3
×(3+3 )×6
)×6 =9
=9 +18.
+18.
∴当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9 +18.
+18.
(3)①如图,过C点作CF⊥x轴于F,
∵OC∥AD,
∴∠ADO=∠COD=90°,
∴∠DOA+∠DAO=90°
而∠DOA+∠COF=90°,
∴∠COF=∠DAO,
∴Rt△OCF∽Rt△AOD,
∴ =
= ,即
,即 =
= ,解得CF=
,解得CF= ,
,
在Rt△OCF中,OF= =
= ,
,
∴C点坐标为(﹣ ,
, );
);
②直线BC是⊙O的切线.理由如下:
在Rt△OCF中,OC=3,OF= ,
,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
∵在△BOC和△AOD中
 ,
,
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADC=90°,
∴OC⊥BC,
∴直线BC为⊙O的切线.

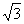 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
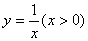 和
和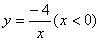 如图所示,
如图所示, 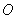 为坐标原点.直线AB:
为坐标原点.直线AB: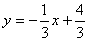 分别于它们交于A,B两点。 过点作
分别于它们交于A,B两点。 过点作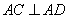 交抛物线于点
交抛物线于点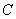 ,过点
,过点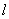 交线段
交线段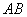 于点
于点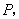 设
设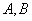 到直线
到直线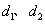 ,则
,则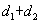 的最大值为__ __.
的最大值为__ __.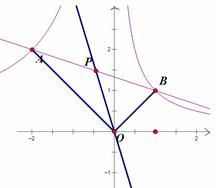
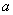 (单位:cm),点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N。点M从点C出发,以1cm/s的速度沿CD向点D运动,点E从点A出发,以
(单位:cm),点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N。点M从点C出发,以1cm/s的速度沿CD向点D运动,点E从点A出发,以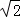 cm/s速度沿AC向点C运动,运动时间为
cm/s速度沿AC向点C运动,运动时间为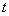 (
(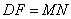 ;
;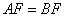 时,点M是边CD的三等分点;
时,点M是边CD的三等分点;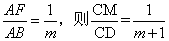
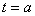 或
或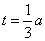 时,
时,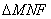 为等腰三角形;
为等腰三角形;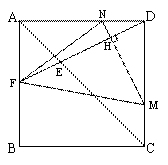
 时,函数
时,函数 ,在x
,在x 时,y都随x的增大而增大吗?请写出你的判断,并说明理由。
时,y都随x的增大而增大吗?请写出你的判断,并说明理由。
 丨+
丨+ = .
= . 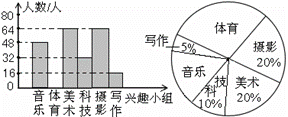 A.七年级共有320人参加了兴趣小组;
A.七年级共有320人参加了兴趣小组;  经过O、C两点,并将抛物线的顶点记作P.
经过O、C两点,并将抛物线的顶点记作P. (1)求证:
(1)求证: ;
; 的取值范围;
的取值范围; 只有一个公共点,请你判断四边形CMPE的形状,并说明理由.
只有一个公共点,请你判断四边形CMPE的形状,并说明理由.