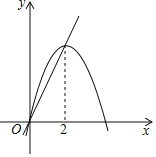��Ŀ����
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���y����x2+2|x|+1��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�
x | �� | ��3 | �� | ��2 | ��1 | 0 | 1 | 2 |
| 3 | �� |
y | �� | ��2 | �� | m | 2 | 1 | 2 | 1 | �� | ��2 | �� |
����m���� ����
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�����˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
��3���۲캯��ͼ��д���������������ʣ�
��4����һ��̽������ͼ���֣�
�����̩�x2+2|x|+1��0���� ����ʵ������
������x�ķ��̩�x2+2|x|+1��
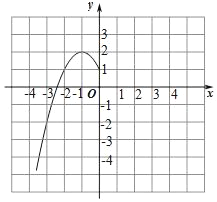
���𰸡���1��1����2�������������3�������������ֵ��2��û����Сֵ������x��1ʱ��y��x���������С����4����2����1��a��2��
��������
��1�����ݶԳƿɵ�m=1��
��2������ͼ�Σ�
��3����д���������ֵ����Сֵ���⣻
��ȷ��һ����Χд���������⣻
��4���ٵ�y=0ʱ����x��Ľ���������������2��ʵ������
�ڵ�y=aʱ����4��ʵ����������4�����㣬ȷ����a��ֵ���ɣ�
�⣺��1���ɱ����֪��ͼ��ĶԳ�����y�ᣬ
��m��1��
�ʴ�Ϊ��1��
��2����ͼ��ʾ��
��3�����ʣ������������ֵ��2��û����Сֵ��
����x��1ʱ��y��x���������С��
��4������ͼ��ã���������x������������
��̩�x2+2|x|+1��0��2��ʵ������
�ʴ�Ϊ��2��
����ͼ���֪����x2+2|x|+1��a��4��ʵ����ʱ��
��y��aʱ����ͼ����4�����㣬
����a��ȡֵ��Χ�ǣ�1��a��2��
�ʴ�Ϊ��1��a��2��

����Ŀ���ڵ������ڣ����ɹ�������ɵij������������������֮��Ĺ�ϵ���±���
�������������/ǧ�� | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
���ɵij���/ | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
��1�����ɲ�������ʱ�ij����Ƕ��٣�
��2�������![]() ��ʾ���������������������
��ʾ���������������������![]() ��ʾ���ɵij��ȣ�д��
��ʾ���ɵij��ȣ�д��![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��3�������ʱ������������Ϊ25ǧ�ˣ�����Ԥ�����Ϊ14ǧ��ʱ�����ɵij����Ƕ��٣�