Question

【题目】如图，在△ABC中，AB=AC=5，BC=6，将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C．若点A′恰好落在BC的延长线上，则点B′到BA′的距离为 ．

Answer 1

【答案】
【解析】解：作A′D⊥CB′于D，B′E⊥BC于E，如图，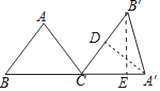
∵△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C，
∴A′B′=A′C=AB=AC=5，B′C=BC=6，
∴CD=B′D= B′C=3，
在Rt△A′CD中，A′D= =4，
∵ B′EA′C= A′DB′C，
∴B′E= = ，
即点B′到BA′的距离为 ．
故答案为 ．
作A′D⊥CB′于D，B′E⊥BC于E，如图，利用旋转的性质得A′B′=A′C=AB=AC=5，B′C=BC=6，再根据等腰三角形的性质得CD=B′D= B′C=3，则利用勾股定理得到A′D=4，然后利用面积法求B′E．