题目内容
已知,如图,⊙O直径AB延长线上一点P,割线PCD交⊙O于C,D. 弦DF⊥AB于H,CF交AB于E,DE⊥CF,∠P=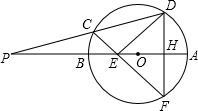 15°,⊙O的半径为2,则CF的大小为
15°,⊙O的半径为2,则CF的大小为
- A.

- B.

- C.
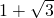
- D.
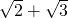
B
分析:利用垂径定理得出∠AOD=∠DCF,进而证明△DHE是等腰直角三角形,进一步证明△DEO∽△DEC,从而求出答案.
解答:∵AB是⊙O的直径,DF⊥AB于D点H,
∴ =
=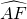 =
= ,
,
∴∠1=∠2,
即:∠AOD=∠DCF
∴AB是弦DF的垂直平分线
∴DE=EF,
∴∠3=∠4,
∵DE⊥CF,
∴∠3=∠4=45°,
∴∠4=∠5=45°,
∵∠P=15°,
∴∠1=60°,
在Rt△DHO中,
∵∠1=60°,OD=2,
∴OH=1,DH= ,
,
∵△DHE是等腰直角三角形
∴DE= ,
,
又∵∠1=∠2,∠DHO=∠DEC=90°,
∴△DEO∽△DEC
∴ ,
,
∴EC= ;
;
∴CF=CE+EF=CE+DE= +
+ .
.
故选B.
点评:此题主要考查了垂径定理与圆周角定理和解直角三角形以及等腰三角形的性质与判定等知识,综合性较强得出△DEO∽△DEC是解决问题的关键.
分析:利用垂径定理得出∠AOD=∠DCF,进而证明△DHE是等腰直角三角形,进一步证明△DEO∽△DEC,从而求出答案.
解答:∵AB是⊙O的直径,DF⊥AB于D点H,

∴
 =
= =
= ,
,∴∠1=∠2,
即:∠AOD=∠DCF
∴AB是弦DF的垂直平分线
∴DE=EF,
∴∠3=∠4,
∵DE⊥CF,
∴∠3=∠4=45°,
∴∠4=∠5=45°,
∵∠P=15°,
∴∠1=60°,
在Rt△DHO中,
∵∠1=60°,OD=2,
∴OH=1,DH=
 ,
,∵△DHE是等腰直角三角形
∴DE=
 ,
,又∵∠1=∠2,∠DHO=∠DEC=90°,
∴△DEO∽△DEC
∴
 ,
,∴EC=
 ;
;∴CF=CE+EF=CE+DE=
 +
+ .
.故选B.
点评:此题主要考查了垂径定理与圆周角定理和解直角三角形以及等腰三角形的性质与判定等知识,综合性较强得出△DEO∽△DEC是解决问题的关键.

练习册系列答案
相关题目

 长交y轴于点D(0,3)
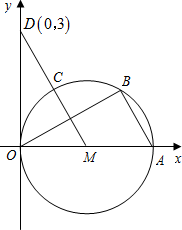
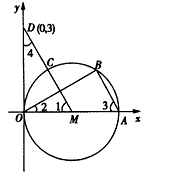
长交y轴于点D(0,3)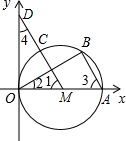 已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3) 分为三等份,连接MC并延长交y轴于点D(0,3)。
分为三等份,连接MC并延长交y轴于点D(0,3)。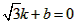 。
。 
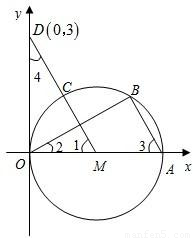
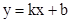 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.